Introduction
Mathematicians, economists, statisticians and others have applied their skills to manage problems for many years. The first concerted and dramatically successful effort in their areas occurred during World War II when specialists were formed into operations analysis groups to assist in planning military operations. These analysts used mathematics and statistics extensively in their studies, and their resulting recommendations were an important contribution to the war effort. Following the war, analysts, soon joined by others, turned their attention and their new techniques to attacking problems of manage mental operations. They accomplished major improvement in inventory control, quality control, warehouse location, industrial operations, agriculture, purchasing decisions, scheduling complex tasks and a variety of others.
A Real World Case
Food is related to the primary needs of human being. To fulfill this need we cultivate different types of crops and make a variety of foods such as bread, biscuits, soft drinks, tea, coffee, and different sorts of junk foods. For making these foods many restaurants, hotels, bakeries etc. are established in a large number.
A few days back, we visited such a type of food making factory to gather different information of their production to apply mathematical calculations which we learnt from our course- ‘Business Mathematics I.’ When we visited the factory we were welcomed warmly by its’ owner and workers. They helped us by giving a variety of information we asked them.
A brief description of the factory and information supplied by its’ owner and workers are given below:
1 Name of the factory: Rana Bread
2 Address: 10/B Vagalpur Lane, Hazaribag, Dhaka-1209
3 Owner: Md. Ariful Qader Rana
4 Date of establishment: November 2
5 Type of business: Small industry
6 Fixed Cost:
| Description
| Amount (Tk.) |
| Land | 50000 |
| Machinery | 40000 |
| Equipment | 20000 |
| Vehicle | 24000 |
| Building | 14000 |
| Gas line | 5200 |
| Others | 1300 |
| Total | 154500 |
7 Variable cost per unit: Tk. 5
8 Selling price per unit: Tk. 15
9 Financing method:
| Description | Amount (Tk.) |
| Own | 54500 |
| Loan from relatives | 40000 |
| Bank loan | 60000 |
| Total | 154500 |
→ Loan from relatives is @ 10% simple interest
→ Bank loan is @ 12% compound interest
10 Units sold (last 6 months):
| Name of the month | Units |
| November 2009 | 16000 |
| December 2009 | 17500 |
| January 2010 | 18000 |
| February 2010 | 20000 |
| March 2010 | 22000 |
| April 2010 | 25000 |
| Total | 118500 |
→ 8% of the volume of sales is selling expense.
11. Usage of gas ( last 6 months):
| Name of the month | Cu.Feet | Units |
| November 2009 | 1600 | 16 |
| December 2009 | 1700 | 17 |
| January 2010 | 1800 | 18 |
| February 2010 | 2000 | 20 |
| March 2010 | 2200 | 22 |
| April 2010 | 2500 | 25 |
| Total | 11800 | 118 |
→ Rana Bread took the gas line from Titas Gas Co. which charges its’ customers- Tk. 350 as customer charge; Tk. 2.5 per unit (100 cubic feet) for the first 20 units; and Tk. 1.25 per unit each unit over 20.
12. Depreciation of machinery: Rana Bread depreciates its’ machinery in value 10% applied to the original
13. Depreciation of equipment: Rana Bread depreciates its’ equipment in value, 15% in November 2009, 12.5% in December 2009, 10% in January 2010 and so on; all percentages applying to the original cost.
After visiting Rana Bread we came to know about some important information on how one can make his/her desire come true. Rana Bread, though established a few months ago, is running its’ production and marketing activities quite impressively and making profit in an increasing percentage.
Application of mathematics in Rana Bread
There is currently a strong trend toward incorporating technology into the teaching of mathematics. Electronic tools include basic calculators, programmable calculators, graphic calculators and computer algebra system (CAS). The effective use of this technology allows the individual to focus more on application, problem formulation, and the interpretation of numerical and graphical results.
As we said earlier, our main aim is to apply mathematics in business to implement our theoretical knowledge practically, so now we are trying our best to apply different mathematical terms in the information of Rana Bread which we got during the our visit to it.
Break-even interpretation I
From the case e came to know that,
Fixed cost= Tk.154500
Variable cost= Tk. 5 per unit
Selling price= Tk. 15 per unit
We denote the number (quantity) of breads made and sold by q. Then since bread are sold at Tk.15 per unit, the revenue function is
R (q) = 15q
Now since the variable cost per unit is Tk.5, the variable cost of making q units will be 5q. Adding the fixed cost of Tk. 154500, the cost function becomes
C (q) = 5q+154500
Lastly, since profit is revenue minus cost, the profit function is
P (q) = R (q) – C (q)
= 15q – (5q + 154500)
= 10q -154500
Notice that the coefficient 10 of q represents the profit per unit and is precisely the difference between the selling price per unit of Tk.15 and the variable cost per unit of Tk. 5. Similarly, the constant term of
-154500 indicates that the manufacturer has to produce and sell enough units of breads to compensate for the fixed cost of Tk.154500 before breaking even.
One way for the owner of a business to make sure he/she is making a profit is to first analyze the circumstances necessary to break even (i.e. neither make a profit nor suffer a loss). Then the owner can develop a plan to do better than break-even (i.e. make a profit). Now to break-even simply means the revenues must equal costs, so since
Profit = Revenue – Cost
Then at break-even
Revenue = Cost
Means that
Profit = 0
So, at break-even profit will be 0. Thus
P (q) = 0
→ 10q – 154500 = 0
→ q = 154500÷10 units
→ q = 15450 units
Finally, the break-even taka volume of sales (revenue) is
R (15450) = 15×15450
= Tk. 231750
Break-even chart I
Returning to the revenue and cost functions of Rana Bread,
R (q) = 15q and C (q) = 5q+154500
And plotting these in the usual manner, we obtain the graphs in Figure-1. Observe that the revenue line goes through the origin and the cost line has a y-intercept of Tk. 154500.
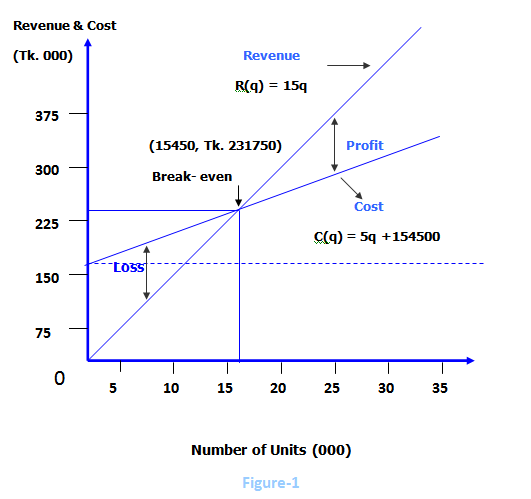
The dotted horizontal line shows that the fixed cost is constant at all levels of operation of the factory. The variable cost which is the 5q in the cost function is the vertical distance from the fixed cost line to the total cost line; it increases as more units are produced. To the left of the break-even point (15450, Tk. 231750), the cost line is above the revenue line; the vertical separation at any points represents the associated loss. On the other hand, to the right of the break-even point (15450, Tk.231750), the vertical separation represents the associated profit.
Break-even interpretation II
Production managers and other operations executives tend to think of break-even analysis in the way that we presented in the previous section. Controllers and other financial managers are more likely to think in accounting terms. To illustrate this latter way of viewing break-even, we shall consider that Rana Bread produces and sells its’ bread at a price that is presumably above the cost.
From the case of Rana Bread stated earlier we came to know that
Total cost = Fixed cost + Variable cost
= 154500+5(118500)
= 747000
Total selling price = 15×118500
=1777500
As we know that mark-up is the difference between the selling price and the cost, so
Mark-up = Selling price – cost
=1777500-747000
=10305000
Now, as margin is the mark-up as a percentage of the selling price, so margin of Rana Bread will be
Margin = Mark-up ÷ Selling price
=10305000 ÷ 1777500
=0.58 or 58%
This means that 58% of the selling price of Tk. 1777500 is margin, and the other 42% of Tk. 1777500 which is,
0.42×1777500=746550,
is the cost.
We, now, suppose that Rana Bread uses a margin of 58% on all items it produces, so that if it sells Tk.s – worth of products, 58% of this amount is margin and 42% is the cost.
Thus,
Cost of goods sold = 0.42s
In the case
Selling expense = 8% of sales
= 0.08
Fixed cost = 154500
So the total cost function is
C(s) = 0.42s+0.08s+154500
=0.50s+154500
Now, if Rana Bread sells Tk.s –worth of products, its’ revenue will clearly be the same Tk.s. So that the revenue function is
R(s) = s
Since profit is still revenue minus cost, the profit function is
P(s) = R(s)-C(s)
= s-(0.50s+154500)
= 0.50s-154500
Notice that the coefficient 0.50 of s represents the profit per taka of sales, it is precisely the difference between each Tk. 1.00 of sales and the associated Tk.0.50 cost per taka of sales. Alternatively, the 0.50 can be viewed as the difference between the Tk. 0.58 margin per taka of sales and the Tk. 0.08 selling expense per taka of sales. As before, the constant term of -154500 indicates that Rana Bread has to sell Tk. 154500 worth of products to compensate for the fixed cost of Tk. 154500.
Now, as before, break-even will occur when profit is 0. That is
P(s) = 0
→0.50s-154500=0
→s=309000
So, Rana Bread must target a sales of at least Tk. 309000 just to be assured of breaking even.
Break-even chart II
Returning to the revenue and cost functions of Rana Bread
R(s)=s and C(s)=0.50s+154500
and plotting this in the usual manner, we obtain the graphs in Figure-2.
Revenue & Cost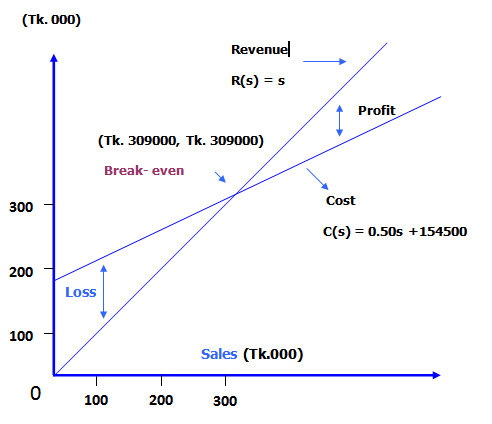
The point of intersection (Tk. 309000, Tk. 309000) of revenue function R(s) and the cost function C(s) establishes the break-even level of sales. The separation of lines to the right of break-even indicates profit. On the other hand, the separation of lines to the left of break-even shows loss.
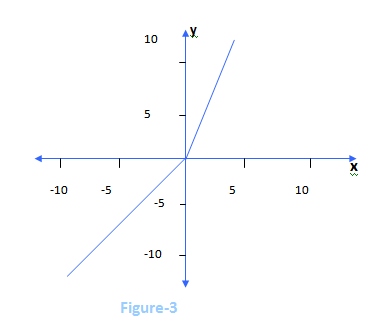
Piecewise linear functions
Sometimes an equation will consist of more than one section or piece, each of which is linear. For example,
x ; x≤0
y= 2x ; x>0
describes a function composed of two linear pieces, the first being x for all values of x≤0, and the second being 2x for all values of x>0. Such a function is a piecewise linear function and its’ graph is shown in Figure-3.
The charge for the first 20 units consists of the Tk. 350 customer charge plus the Tk. 2.5 charge per unit. Letting u represent the number of units used, this charge becomes
2.5u+350…………………….(1)
Now if Rana Bread uses more than 20 units, the charge from (1) for the first 20 units will be
2.5(20)+350=400
To this must be added the charge of Tk. 1.25 for each unit over 20, resulting in a charge of
400+1.25(u-20)
= 400+1.25u-25
=1.25u+375…………………… Putting (1) and (2) together, we get the cost function
C(u) = 2.5u+350; 0≤u≤20
C(u)= 1.25u+375; u>20
Figure-4 graphs this function.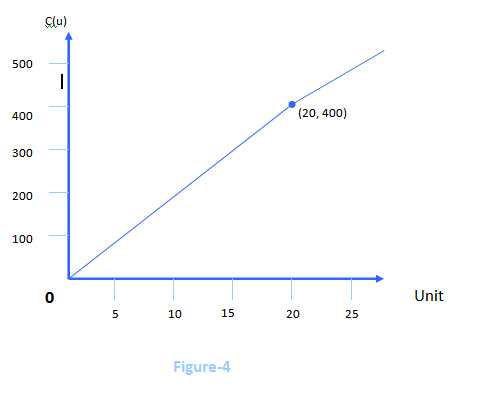
Cost of November 2009, when 16 (<20) units of gas were used,
C(u) = 2.5u+350
=2.5(16)+350
=40+350
=390
Cost of December 2009, when 17 (<20) units of gas were used,
C (u) =2.5u+350
=2.5(17)+350
=42.5+350
=392.50
Cost of January 2010, when 18 (<20) units of gas were used,
C (u) =2.5u+350
=2.5(18)+350
=45+350
=395
Cost of February 2010, when 20 (=20) units of gas were used,
C (u) = 2.5u+350
=2.5(20)+350
=50+350
=400
Cost of March 2010, when 22 (>20) units of gas were used,
C (u) =1.25u+375
=1.25(22)+375
=27.5+375
=402.50
Cost of April 2010, when 25 (>20) units of gas were used,
C (u) =1.25u+375
=1.25(25)+375
=31.25+375
=406.25
Now potting these costs of last six months of Rana Bread we find the graphs in Fgure-5 which is a graph of piecewise linear functions.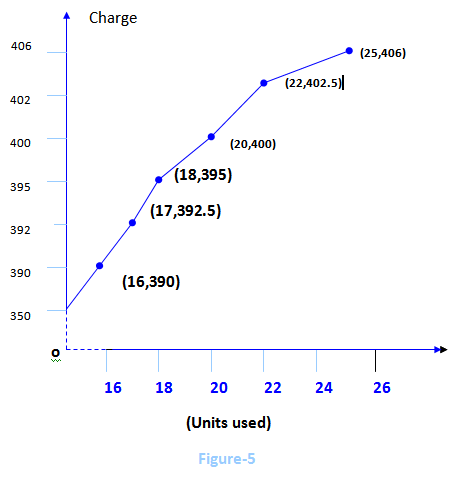
Simple interest
In the case of Rana Bread stated earlier the owner has taken a loan of Tk. 40000 @ 10% in the month of November 2009 from his relatives.
Here
Amount of loan (P) = 40000
Interest rate (i) = 10% or 0.10
Time passed (n) = 6 months
=6/12
=0.50
So, the amount with interest to be paid if the loan is returned at the end of April 2010.
A = P (1+in)
=40000 (1+0.10×0.50)
=40000 (1.05)
=42000
Interest of last six months (Nov.’09-April ’10)
A-P
= 42000-40000
=2000
and interest of each month
Interest ÷Time passed
= 2000÷6
=333.33
Compound interest
In the case of Rana Bread stated earlier the owner has also taken a loan of Tk. 60000 @ 12% at the same time from the bank.
Here
Amount of loan (P) = 60000
Interest rate (i) = 12% or 0.12
For the month of November 2009
P = 60000
i= 0.12
n = 1/12 or 0.08
Net amount, A = P (1+0.12)n
=60000(1+0.12)0.08
=60546
Interest =60546-60000
=546
For the month of December 2009
P = 60546
i = 0.12
n= 0.08
Net amount, A = 60546 (1+0.12)0.08
= 61097
Interest = 61097-60546
= 551
For the month of January 2010
P= 61097
i=0.12
n=0.08
Net amount, A= 61097(1+0.12)0.08
=61653
Interest =61653-61097
=556
For the month of February 2010
P=61653
i= 0.12
n=0.08
Net amount, A = 61653(1+0.12)0.08
=62215
Interest = 62215-61653
=562
For the month of March 2010
P=62215
i=0.12
n=0.08
Net amount, A =62215(1+0.12)0.08
=62782
Interest =62782-62215
=567
For the month of April 2010
P=62782
i=0.12
n=0.08
Net amount, A=62782(1+0.12)0.08
=63354
Interest = 63354-62782
=572
Salvage value
Rana Bread uses machinery for its’ production. The machinery has a
Cost (C) = 40000
Depreciation rate (d) = 10% or 0.10
Depreciation period (n) = 6 months
= 6/12 or 0.50
So, after six months the salvage value of the machinery used by Rana Bread will be
S = C (1-d)n
=40000 (1-0.10)0.50
=40000 (0.90)0.50
=37947.33
=37947
So, if the machinery of Rana Bread is sold right now (i.e. after being used for six months) the salvage value of the machinery would be Tk. 37947.
Arithmetic progression
An arithmetic progression is a sequence whose terms increase or decrease by a constant number called the common difference. A series in arithmetic progression thus becomes an additive series in which the common difference can be found by subtracting each term from its’ preceding one.
Thus if the first term and the common difference are known, the A.P. is completely known.
The arithmetic progression
a, (a+d), (a+2d), (a+3d),…………………
whose first term is a the common difference is d, is designated as the standard form of an arithmetic progression.
The corresponding arithmetic series
a+(a+d)+(a+2d)+(a+3d)+…………………….
is designated as the standard form of an arithmetic series.
A.P. in Rana Bread
Suppose the cost of the equipment used by Rana Bread is Tk. 100. Now the percentages of depreciation at the end of November 2009, December 2009, January 2010 and so on are respectively 15, 12.5, 10,…………. which are arithmetic progression with
a = 15
d = 12.5-15 = -2.5
n = 6
Hence, percentages of depreciation in April 2010,
a+ (n-1)d
= 15+(6-1)(-2.5)
= 15+5(-2.5)
= 15-12.5
= 2.5
So, the A.P. series of depreciation of equipment for six months
15+12.5+10+…………+2.5
Also, total value of equipment depreciated in six months
n/2 (a+l)
= 6/2 (15+2.5)
= 3 × 17.5
= 52.5
Hence, the value of equipment of Rana Bread at the end of April 2010
100-52.5
= 47.5
Now the total cost being Tk. 20000, the value of Rana Breads’ equipment at the end of April 2010
(Tk. 20000÷100)×47.5
= Tk. 9500
Conclusion
Mathematics, an ancient method of calculation, can be used by any one in solving different types of problems. As technology is developing very fast different applications of mathematics now can be done easily within a very short time using modern calculating devices. Whereas, the typical mathematics takes a longer time than the modern devices take. Although we can do our necessary calculations using modern calculating devices, we should try to know and use the typical mathematical terms to enrich our mathematical knowledge.