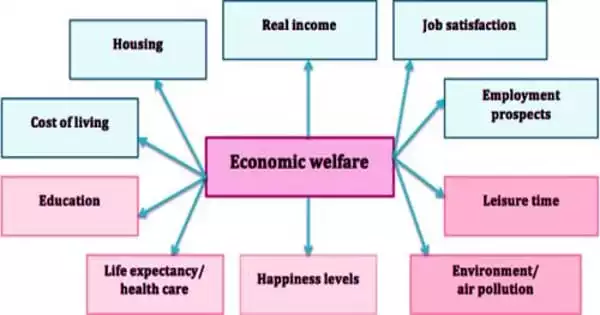
The study of how the allocation of resources and goods affects social welfare is known as welfare economics. A social welfare function is a function in welfare economics that ranks social states (alternative complete descriptions of society) as less desirable, more desirable, or indifferent for every possible pair of social states. It is concerned with the economically efficient distribution of resources for the benefit of the people. This is directly related to the study of economic efficiency and income distribution, as well as how these two factors affect people’s overall well-being in the economy. The function’s inputs include any variables thought to affect a society’s economic well-being.
Welfare economics is a branch of economics that studies the structure of the economy and the markets that comprise it in order to achieve an efficient allocation of goods and resources in society.
The social welfare function is individualistic in nature because it uses welfare measures of individuals in society as inputs. In practice, welfare economists seek to provide tools to help guide public policy in order to achieve positive social and economic outcomes for all members of society. A social welfare function can be used to represent prospective patterns of collective choice between alternative social states. However, welfare economics is a subjective study that is heavily reliant on selected assumptions about how welfare can be defined, measured, and compared for individuals and society as a whole. The social welfare function provides the government with a simple guideline for achieving the optimal distribution of income.
The goal of welfare economics is to improve society’s overall well-being. As a result, welfare economics entails evaluating economic policies and guiding public policies for the greater good of society. The tools of cost-benefit analysis and social welfare functions are used in the study of welfare economics. The study’s underlying assumptions are the measurability and comparability of social welfare across various segments of society, as well as ethical and philosophical concerns about social well-being.
The application of utility theory in microeconomics is the starting point for welfare economics. The perceived value of a particular good or service is referred to as utility. The social welfare function is analogous to the consumer theory of indifference-curve–budget constraint tangency for an individual, except that the social welfare function is a mapping of everyone in the society’s individual preferences or judgments as to collective choices that apply to all, whatever individual preferences are for (variable) constraints on factors of production.
One purpose of a social welfare function is to determine how close the analogy is to an ordinal utility function for an individual with at least minimal welfare economic constraints, such as constraints on the number of factors of production. It entails employing utility theory in economics. The value perceived by the society of the goods and services offered to society is referred to as utility. According to the utility theory, consumers will seek to maximize their utility through their actions as buyers and sellers in accordance with the laws of demand and supply.