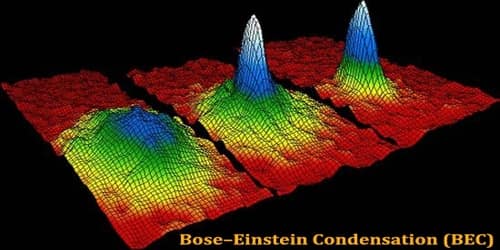
The Concept of Bose-Einstein Condensation (BEC)
Bose-Einstein condensation (BEC), a state of matter in which separate atoms or subatomic particles, cooled to near absolute zero (0 K, − 273.15 °C, or − 459.67 °F; K = Kelvin), coalesce into a single quantum mechanical entity—that is, one that can be described by a wave function—on a near-microscopic scale.
Back in the 1920s, Albert Einstein and Indian theoretical physicist Satyendra Nath Bose predicted that quantum mechanics could force a large number of particles to behave in concert as a single unit, one massive particle. Almost 100 years later, the first Bose-Einstein condensate was created from a gas of alkali atoms!
BEC theory traces back to 1924 when Bose considered how groups of photons behave. Photons belong to one of the two great classes of elementary or submicroscopic particles defined by whether their quantum spin is a non-negative integer (0, 1, 2, …) or an odd half-integer (1/2, 3/2, …). The former type, called bosons, includes photons, whose spin is 1. The latter type, called fermions, includes electrons, whose spin is 1/2.
The result of the efforts of Bose and Einstein is the concept of a Bose gas, governed by the Bose-Einstein statistics, which describes the statistical distribution of identical particles with integer spin, now known as bosons (such as the photon and helium-4). In Bose-Einstein statistics, any number of identical bosons can be in the same state. In particular, given an energy state ε, the number of non-interacting bosons in thermal equilibrium at temperature T = 1/β is given by the Bose occupation number.
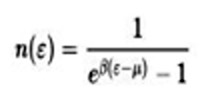
where the constant μ is determined by an equation describing the conservation of the number of particles
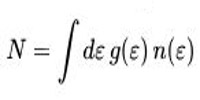
with g(ε) being the density of states of the system.
This last equation may lack a solution at low enough temperatures when g(ε) → 0 for ε → 0. In this case, a critical temperature Tc is found such that for T < Tc the system is in a Bose-Einstein condensed phase and a finite fraction of the bosons are in the ground state.
BE statistics is that the former applies to identical particles that are distinguishable from one another in some way, while the latter describes identical indistinguishable particles. Bose-Einstein statistics assume that, for a given temperature, all quantum states have equal “a priori” probabilities. From this assumption, one can derive the Bose-Einstein distributed occupation number for a quantum state at energy E when the system is held at temperature T.
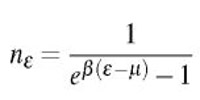
where we used the short-hand notation β = 1/kBT. The chemical potential fl is an important parameter of the system, which helps to normalize the distribution to the total number of particles,
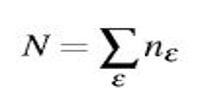
Similarly, the total energy of the system is given by
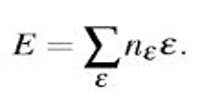
Information Source: