ALAMOUTI Space Time Block Code for MIMO System
Introduction
An overview of the channel capacities under different scenarios. Single input single output wireless channel capacity is considered first. Multiple channel capacity studies are inspected. MIMO capacity for different conditions is considered. Multi-Input Multi-Output communication system consisting of the following identities. s input symbols to be transmitted, Nt the number of transmit antennas, Nr the number of receiver antennas y the received symbol vector, H Nr x Nt MIMO channel matrix n noise with covariance matrix, E{nH}=N0INr
Capacity in AWGN
Capacity studies in communication started with Claude Shannon pioneered theorems. He defined capacity as the maximum mutual information between inputs and outputs of a communication channel. He then defined his coding theorem, which states that a code does exist that could achieve a data rate close to the capacity with a negligible probability of error. Shannon studies were related to the AWGN channel, wire lined channels. These channels do not fade the signals. Considering the wireless transmission, it is expected that the maximum supportable capacity is smaller than that of the wire lined channels. This is due to the multi-path and fading effects of the wireless communication channels. Capacity studies initially are done for flat fading channels.
The capacity of AWGN channel given the Bandwidth B and SNR g is given by the well known formula.
C=Blog2 (1+ g)
Shannon capacity can be considered as an upper limit for real systems. In wireless communication channel-fading information is important to be known at the transmitter or receiver side for better communication.
Capacity of Multi-channel Communications
Consider a Multi-Input Multi-Output communication system consisting of the following identities:
- s input signal to be transmitted,
- Nt the number of transmit antennas,
- Nr the number of receiver antennas
- y the received signal vector,
- H is the channel response in the Nr x Nt MIMO channel matrix
- n noise with covariance matrix, E{nnH}=N0INr
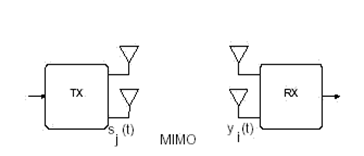
Figure : MIMO Communication system[6]
The relation between input and output is given by
Es is the average transmits signal energy. If we choose Ts=1 then Es turns out to be the transmit power.
Deterministic MIMO channel capacity
Telstra has taken the role of Shannon for MIMO channel capacity studies; he defined the deterministic MIMO channel capacity as stated below
Rss=E{ssH}; Tr(Rss)=Nt
Bps/Hz
Channel knowledge available only at receiver
The channel capacity in the absence of the channel knowledge at the transmitter is given by the following formula.
Rss=INt
Inserting HHH=QDQH in the above equation, an equivalent and simple expression is obtained as in (13)
r
C = ∑ Log2(1+ES /NtNo*λi)
i=1
r is the rank of the channel and lis are the positive eigenvalues of the HHH
In the case of an normalized orthogonal channel satisfying Nr=Nt=N, the capacity of the MIMO channel is given as
C = N log2 (1+ (Es/No))
That is the capacity of MIMO channel is equal to N times that of the SISO channel.
Channel knowledge available at the transmitter side case:
Figure 4.2: System model when channel knowledge is available at the transmitter side[6]
SVD of H yields H= UVH, inserting this into (11) and rearranging the parameters we get, Or this equation can be written as,
I=1..r, where r is the rank of HHH
The capacity of the MIMO channel is the sum of the SISO channels,
Considering transmit power constraint the capacity formula reduces to,
The capacity maximization problem can be solved using the lagrangian methods, hence leading to the results
The optimal power allocation to the individual channels is found through an algorithm known as the Water pouring algorithm.
As can be seen from the formulas capacity of the MIMO channels increases when the channel knowledge is available at the transmitter, compared to the case in which receiver only has the channel information.
Capacity of the multiple input single output (MISO) and single input multiple output channels (SIMO).
Random MIMO channel capacity
Since the channel is random so the capacity is. In order to understand the capacity for the fading channels some definitions are needed. These are, ergodic capacity, outage capacity, outage probability,
Capacity is the expected value of the capacity over the distribution of the channel elements. It can be though as the mean information rate.
Outage probability: is the probability that given a transmission rate R and transmit power constraint the channel capacity cannot support a reliable communication
Pout = P(C£ R)
Outage Capacity:
Given an outage probability, the maximum information rate that can be supported by the communication channel is called the outage capacity of the channel.
Capacity when the channel is known only to the receiver is given as:
The capacity when the channel is known to the transmitter is given as:
A lower bound for the capacity is defined as [1],
MIMO channel capacity in the presence of antenna correlation effect [8]
When there is correlation between antennas at receiver or transmitter side, the channel matrix is expressed as,
Where Rr and Rt are positive definite matrices showing the correlation effect between antenna elements. The elements of the R matrices can be found using
At high SNR the capacity of the MIMO channel can be written as
Frequency selective MIMO channel capacity [6]
If the channel is frequency selective, then the channel is divided into frequency flat sub-channels and the capacity of the each sub-channel is calculated using the frequency flat channel capacity formulas. The capacity of the frequency selective channel is the sum of each individual frequency flat channel. When the channel knowledge is available at the transmitter side, frequency flat channels uses the water pouring algorithm to distribute the power to the channel modes. In frequency selective channels, power must be distributed across space and frequency to make a more reliable communication. For deterministic frequency selective channels the capacity formula is given as in
If the channel is random then the capacity for the frequency selective MIMO channel is defines as in .
Mutual Information and Shannon Capacity
Channel capacity was established by Claude Shannon in 1940s, by using the mathematical theory of communication. The capacity of a channel is denoted by C. The channel capacity C is the maximum rate at which reliable communication can be performed, without any constraints on transmitter and receiver complexity. Shannon showed that for any rate R < C, there exist rate R channel codes with arbitrarily small block error probabilities.
Thus, for any rate R < C and any desired non-zero probability of error ρe, there exists a rate R code that achieves ρe. The code may have a very long block length and encoding and decoding complexity may also be extremely large. The required block length may increase as the desired ρe is decreased or the rate R is increased towards C. Shannon showed that code operating at rates R > C cannot achieve an arbitrarily small error rate. So the error probability of a code operating at a rate above capacity is bounded away from zero. Therefore, the Shannon channel capacity is truly the fundamental limit to communication.
Capacity of MIMO system
MIMO system consists of multiple transmit and receive antennas interconnected with multiple transmission paths. MIMO increases the capacity of system by utilizing multiple antennas both at transmitter and receiver without increasing the bandwidth.
In the situation where the channel is known at both transmitters (Tx) and receiver (Rx) and is used to compute the optimum weight, the power gain in the kth sub channel is given by the kth value. i.e., the SNR for the kth sub channel equals
Where PK is the power assigned to the kth sub channel, λk is the kth value and σ2N is the noise power. For simplicity, it is assumed that σ2N = 1. According to Shannon, the maximum capacity of K parallel sub channels equals
Where M is the number of symbols and means SNR is defined as
Given the set of evalues { λk }, the power PK allocated to each sub channel k is determined to maximize the capacity by using Gallager’s waterfilling theorem such that
Each sub channel is filled up to a common level D, i.e.
With a constraint on the total Tx power such that
Where, PTX total transmitted power. This means that the sub cannel with the highest
Gain is allocated with the largest amount of power. In the case where 1/ λ, k >D then PK =0
When the uniform power allocation scheme is employed, the power PK is adjusted according to
P1 = ⋯ = PK
Thus, in the situation where the channel is unknown, the uniform distribution of the power is applicable over the antennas. So that the power should be equally distributed between the N elements of the array at the Tx, i.e.,
Pn= PTX/N; n=1…..N
Capacity Analysis using Shannon Capacity
MIMO system consists of multiple transmit and receive antennas interconnected with multiple transmission paths. MIMO increases the capacity of system by utilizing multiple antennas both at transmitter and receiver without increasing the bandwidth.
In the situation where the channel is known at both transmitter (Tx) and receiver (Rx) and
is used to compute the optimum weight, the power gain in the kth sub channel is given by the kth value, i.e., the SNR for the kth sub channel equals.
The capacity of MIMO system is given as follows
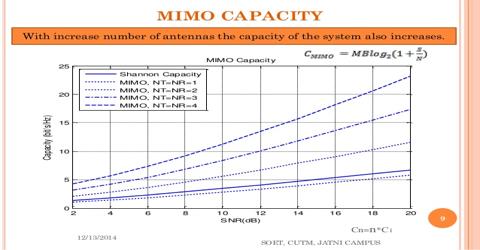
By implementing the above equation using mat lab, following result is obtained
Figure 4.3: Capacity Analysis of MIMO
Observation
Figure 4.3shows, an analysis of the capacity of the system having multiple transmitters and receivers. The capacity of a MIMO system has been plotted against SNR in dB. It is clear that with increase in the number of antennas at the both sides capacity increases linearly i.e. with nt=4 and nr=4, we have achieved highest capacity in MIMO systems.
Summary
MIMO system transmits two or more data streams in the same channel. The data streams are sent at the same time. MIMO System are also used to obtain the goal of evaluating the capacity of a system using N transmit and M receive antennas. Increasing number of antennas at either side of the MIMO system will have same effect in raising the capacity.