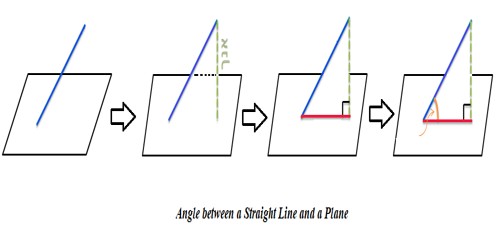
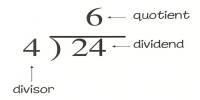Angle between a Straight Line and a Plane:
In mathematics, the term “line” actually refers to the “straight line”. It is a one-dimensional figure that extends in two opposite directions. A straight line can be defined as an interconnected set of an infinite number of points. The length of a line is infinite, while it has zero or no width as well as height.
A normal to the plane is drawn from the point where the line touches the plane. This normal forms an angle with the line. Then, the angle between the line and the plane is equivalent to the complement of the angle between the line and the normal. In this section, we will discuss this concept in detail.
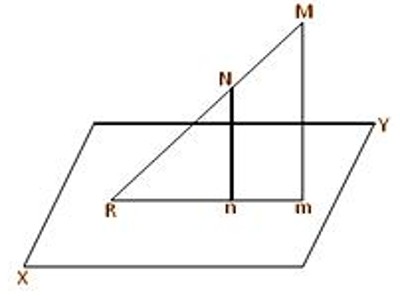
The angle between a straight line and a plane is measured by the angle between the given straight line and its projection on the given plane. Let mn be the projection of the straight line MN on the plane XY. Suppose, in the given figure, straight lines MN and mn (when produced) meet at the point R in the plane XY. Then the angle between the straight line MN and the plane XY is measured by ∠MRm.
A line segment is represented by placing an arrow at each end. Both ends can be named by an uppercase letter. We may also denote a line by a lower case letter (such as l, m, n) which is written on either end of it. In above image, the name of the line segment is PR, whereas the point Q indicates that these three points are collinear.
A plane is said to be a two-dimensional flat figure. It is an extension of a point and a line. When infinite sets of points form together to make a flat surface, it is known as a plane. It extends infinitely in all directions. It does have an infinite length as well as width, but no thickness or height.
Information Source: