Area of a Polygon
A polygon is a two-dimensional shape that is bounded by line segments. It can have as many as finite number of line segments. Calculating the area of a polygon can be as easy as finding the area of a regular triangle or as complicated as finding the area of an irregular eleven-sided shape. Let us discuss about area of polygon.
The total space enclosed within a polygon is known as the area of a polygon. The area of a polygon measures the size of the region enclosed by the polygon. It is measured in units squared. The unit of area is square unit or unit2.
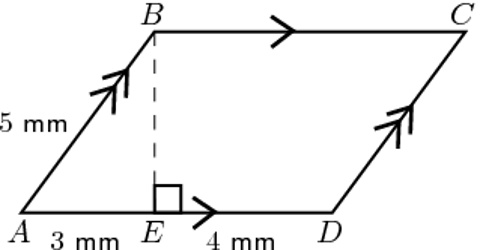
Area of a Regular Polygon
A polygon that has equal sides and equal interior angles, is referred as a regular polygon.
The perpendicular distance from center to any of the side of a regular polygon is known as its apothem or radius of incircle or simply inradius. If the side length of a regular polygon is given, then we can easily find the area of a polygon by the following formula –
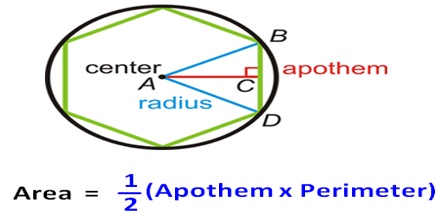
Area of a Regular Polygon = ½ a.p.
- where, a = Apothem
- p = Perimeter of the polygon
We can also write this formula as –
Area of a Regular Polygon = ½ a.n.s.
- where, n = Number of sides
- s = Side length
The area of a regular polygon can also be expressed trigonometrically as –
Area of Regular Polygon = ¼ n 82 cot π/n.
- Where, s = Side length
- and n = Total number of sides
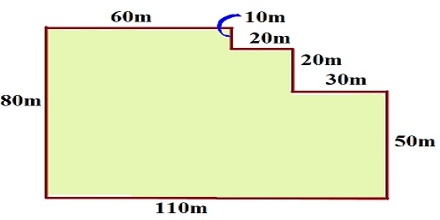
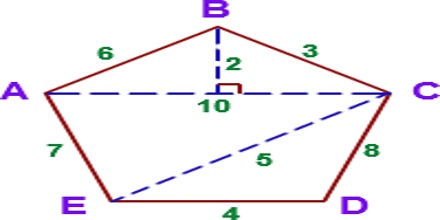
Area of an Irregular Polygon
There is no particular formula for the area of an irregular polygon because it has indefinite shape and size. An incircle or a circumcircle is not possible to draw for an irregular polygon. In order to calculate the area of irregular polygon, it is to be divided into regular polygons by drawing lines from one vertex to others. Then, these areas are to be added to get the required area of polygon.