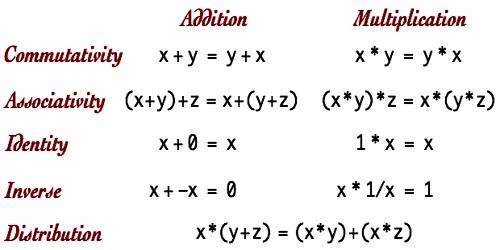Axioms of Algebra
An Axiom is a mathematical statement that is assumed to be true. There are five basic axioms of algebra. Axioms are generally statements made about real numbers. Sometimes they are called algebraic postulates. The axioms are the reflexive axiom, symmetric axiom, transitive axiom, additive axiom and multiplicative axiom.
Reflexive Axiom: A number is equal to itelf. (e.g., a = a). This is the first axiom of equality. It follows Euclid’s Common Notion One: “Things equal to the same thing are equal to each other.”
Symmetric Axiom: Numbers are symmetric around the equals sign. If a = b then b = a. This is the second axiom of equality. It follows Euclid’s Common Notion One: “Things equal to the same thing are equal to each other.”
Transitive Axiom: If a = b and b = c then a = c. This is the third axiom of equality. It follows Euclid’s Common Notion One: “Things equal to the same thing are equal to each other.”
Additive Axiom: If equals are added to equals, then the sums are equal according to the additive axiom. If a = b and c = d then a + c = b + d. If two quantities are equal and an equal amount is added to each, they are still equal.
Multiplicative Axiom: If a = b and c = d then ac = bd. Since multiplication is just repeated addition, the multiplicative axiom follows from the additive axiom. It is sometimes called “the multiplication property of equality.”
Difference between the 5 basic axioms of algebra-
- Reflexive: a = a
- Symmetric: If a = b, then b = a
- Transitive: If a = b and b = c, then a = c
- Additive: If a = b and c = d, then a + c = b + d
- Multiplicative: If a = b and c = d, then a * c = b * d
These 5 basic properties are known truths of algebra. Essentially, they guarantee that numbers equal to the same thing are equal to each other, and that adding an equal number to those 2 equal numbers will result in 2 equal sums.
Information Source: