Triangle is a plane figure with three straight sides and three angles. The three angles always add to 180°. The vertex is a corner of the triangle. Every triangle has three vertices. The interior angles of a triangle always add up to 180°. The exterior angles of a triangle always add up to 360°
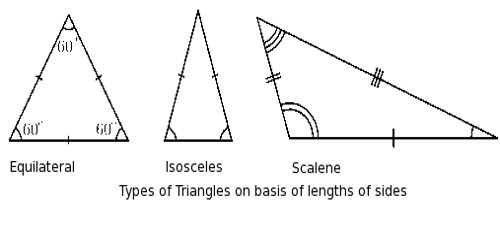
Classification of triangles on the basis of their sides
Equilateral triangle: An equilateral triangle is a triangle whose all three sides are equal. An equilateral triangle is, therefore, a special case of an isosceles triangle having not just two, but all three sides equal. An equilateral triangle also has three equal 60 degrees angles. They are regular polygons, and can therefore also be referred to as regular triangles.
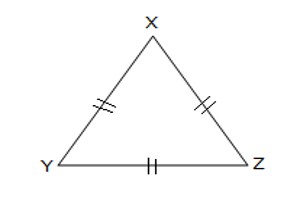
Fig: Equilateral Triangle
Here, XYZ is an equilateral triangle as XY = YZ = ZX.
Isosceles triangle: An isosceles triangle is a triangle whose any two sides are equal. An isosceles triangle, therefore, has both two equal sides and two equal angles. The name derives from the Greek iso (same) and Skelos (leg). Sometimes it is specified as having two and only two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case.
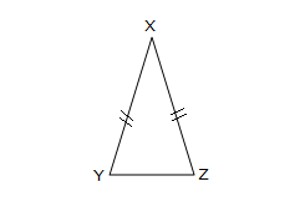
Fig: Isosceles Triangle
The adjoining figure shows an isosceles triangle where XY = XZ.
Scalene triangle: In a scalene triangle, all the three sides are unequal and also no equal angles. The interior angles of a scalene triangle are always all different. The converse of this is also true – If all three angles are different, then the triangle is scalene, and all the sides are different lengths. For example, a triangle with side lengths of 2 cm, 3 cm, and 4 cm would be a scalene triangle. A triangle with side lengths of 2 cm, 2 cm, and 3 cm would not be scalene since two of the sides have the same length.
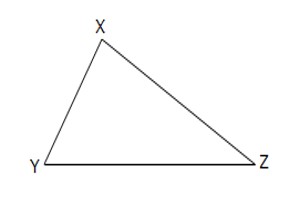
Fig: Scalene Triangle
The above figure shows a scalene triangle where XY ≠ YZ ≠ ZX.
Information Source: