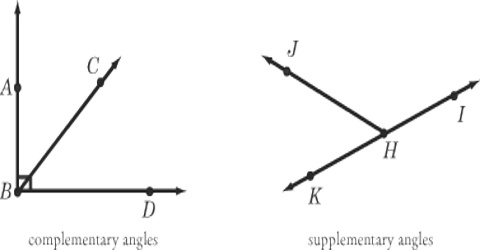
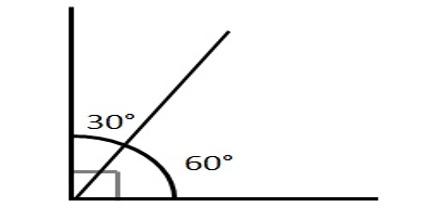
Complementary angles:
Complementary angles are two angles that have a sum of 90°. Two angles whose measures add to 90 degrees. Angle 1 and angle 2 are complementary angles because together they form a right angle. A common case is when they form a right angle.
Note that angle 1 and angle 2 do not have to be adjacent to be complementary as long as they add up to 90 degrees. If the relationship is given, you can subtract the given angle from the sum to determine the measure of the missing angle.
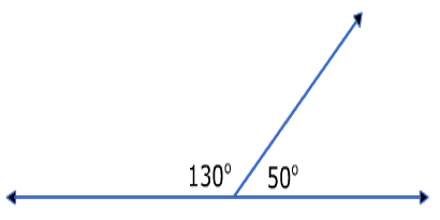
Supplementary angles:
Supplementary angles are two angles that have a sum of 180°. Two angles whose measures add to 180 degrees. The following are supplementary angles. A common case is when they lie on the same side of a straight line.
If the relationship is given, you can subtract the given angle from the sum to determine the measure of the missing angle.
Vertical angles:
Angles that have a common vertex and whose sides are formed by the same lines. The following(angle 1 and angle 2) are vertical angles.
Example: Find angles a°, b° and c° below:
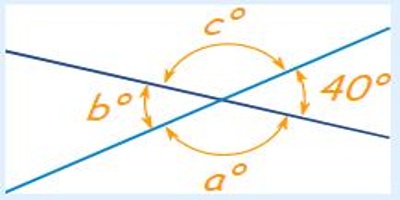
Because b° is vertically opposite 40°, it must also be 40°
A full circle is 360°, so that leaves 360° − 2×40° = 280°
Angles a° and c° are also vertical angles, so must be equal, which means they are 140° each.
Answer: a = 140°, b = 40° and c = 140°.