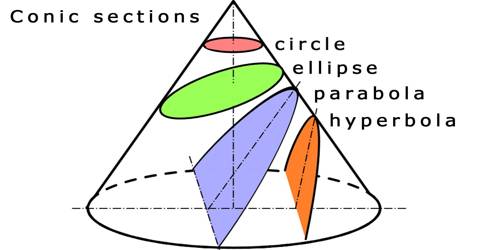
Conic Section: Idea of conic sections as sections of the cone. Focus— Directrix definitions of a conic section, eccentricity, classification according to the value of eccentricity. Depending on the angle of the plane with respect to the cone, a conic section may be a circle, an ellipse, a parabola, or a hyperbola.
A conic section is the intersection of a plane and a double right circular cone. By changing the angle and location of the intersection, we can produce different types of conics. There are four basic types: circles, ellipses, hyperbolas, and parabolas.
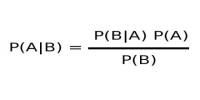
The conic sections of the Euclidean plane have various distinguishing properties. Many of these have been used as the basis for a definition of the conic sections. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a focus, and some particular line, called a directrix, are in a fixed ratio, called the eccentricity. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the set of points whose coordinates satisfy a quadratic equation in two variables. This equation may be written in matrix form, and some geometric properties can be studied as algebraic conditions.

There are three types of conics, the ellipse, parabola, and hyperbola. The circle is a special kind of ellipse, although historically it had been considered as a fourth type (as it was by Apollonius). The circle and the ellipse arise when the intersection of the cone and plane is a closed curve. The circle is obtained when the cutting plane is parallel to the plane of the generating circle of the cone – for a right cone, see diagram, this means that the cutting plane is perpendicular to the symmetry axis of the cone.
Information Source: