Definitions of Sin, Cosine and Tangent
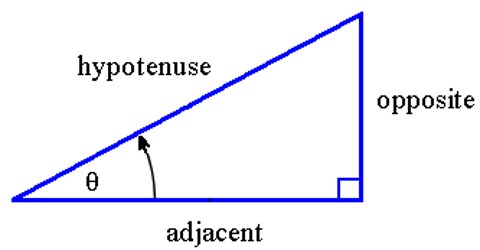
A right triangle consists of one angle of 90° and two acute angles. Each acute angle of a right triangle has the properties of sine, cosine and tangent. Sine, Cosine and Tangent are the main functions used in Trigonometry and are based on a Right-Angled Triangle. The sine, cosine and tangent of an acute angle of a right triangle are ratios of two of the three sides of the right triangle.
The sine of the angle is the ratio of the length of the side opposite the angle divided by the length of the hypotenuse.
The cosine of the angle is the ratio of the length of the side adjacent to the angle divided by the length of the hypotenuse.
The tangent of the angle is the ratio of the length of the side opposite the angle divided by the length of side adjacent to the angle.
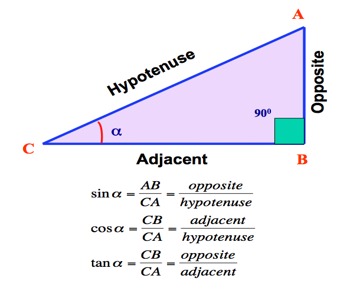
In any right angled triangle, for any angle:
The sine of the angle = [the length of the opposite side / the length of the hypotenuse]
The cosine of the angle = [the length of the adjacent side / the length of the hypotenuse]
The tangent of the angle = [the length of the opposite side/the length of the adjacent side]
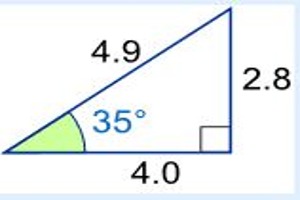
Example: What is the sine of 35°?
Using this triangle (lengths are only to one decimal place):
sin(35°) = Opposite / Hypotenuse = 2.8 / 4.9 = 0.57…
cos(35°) = Adjacent / Hypotenuse = 4.0 / 4.9 = 0.82…
tan(35°) = Opposite / Adjacent = 2.8 / 4.0 = 0.70…
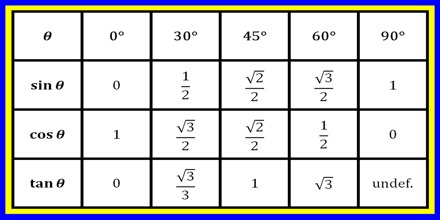
Special Ratio Chart of Sin, Cosine and Tangent: