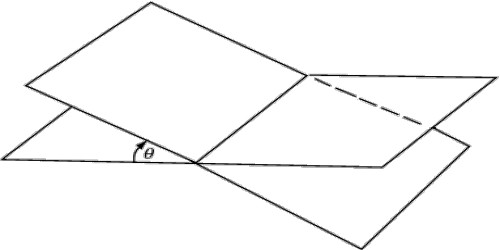
The dihedral angle is an angle between two distinct planes that are intersecting in any way. We can say that the interior angle between two planes is known as a dihedral angle.
The plane angle between two intersecting planes is called a dihedral angle between the planes. It is an angle is the angle between two intersecting planes. The angle between two intersecting planes (i.e., a dihedral angle) is measured as follows: Take any point on the line of intersection of the two planes. From this point draw two straight lines, one in each plane, at right angles to the line of intersection. The angle, which the sides of a dihedral plane separate from a normal plane of the edge, is the normal section of the dihedral angle. If two planes intersect each other and if one of the four dihedral angles formed is right, then also the others are right. Then we say that the planes are perpendicular to each other. Apparently, all normal sections are equal. Then the plane angle between the drawn two lines gives the measure of the dihedral angle between the planes.
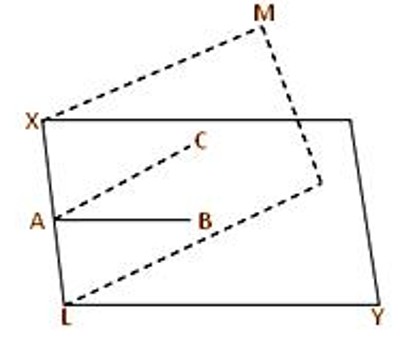
Let XY and LM be two intersecting planes and XL be their line of intersection. From any point, A on XL draw the straight line AB perpendicular to XL in the XY plane and the straight line AC perpendicular to XL in the LM plane. Then the plane ∠BAC is the measure of the dihedral angle between the two intersecting planes XY and LM.
If the dihedral angle between two intersecting planes is a right angle then one plane is said to be perpendicular to the other. In solid geometry, it is defined as the union of a line and two half-planes that have this line as a common edge. In higher dimension, a dihedral angle represents the angle between two hyperplanes.
When the dihedral angle between two planes is zero, it indicates that instead of intersecting, these planes are parallel to each other. Thus, calculating dihedral angle can be very useful in order to prove two planes parallel.
Information Source: