Equality of Complex Numbers
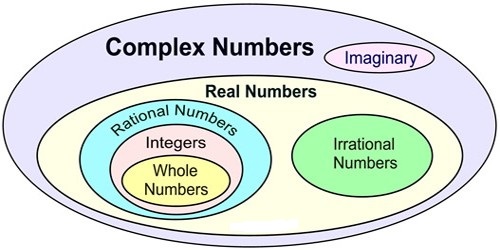
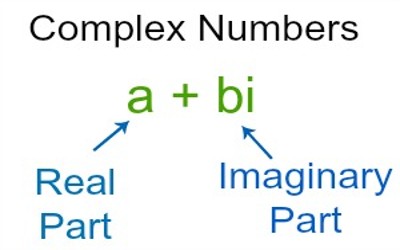
A Complex Number is a combination of a Real Number and an Imaginary Number. A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and ‘i’ is a solution of the equation x2 = −1, which is called an imaginary number because there is no real number that satisfies this equation.
Here discuss the equality of complex numbers-
Two complex numbers z1 = a + ib and z2 = x + iy are equal if and only if a = x and b = y i.e., Re (z1) = Re (z2) and Im (z1) = Im (z2).
Thus, z1 = z2 ⇔ Re (z1) = Re (z2) and Im (z1) = Im (z2).
For example, if the complex numbers z1 = x + iy and z2 = -5 + 7i are equal, then x = -5 and y = 7.
Solved examples on equality of two complex numbers:
- If z1 = 5 + 2yi and z2 = -x + 6i are equal, find the value of x and y.
Solution:
The given two complex numbers are z1 = 5 + 2yi and z2 = -x + 6i.
We know that, two complex numbers z1 = a + ib and z2 = x + iy are equal if a = x and b = y.
z1 = z2
⇒ 5 + 2yi = -x + 6i
⇒ 5 = -x and 2y = 6
⇒ x = -5 and y = 3
Therefore, the value of x = -5 and the value of y = 3.
- If a, b are real numbers and 7a + i(3a – b) = 14 – 6i, then find the values of a and b.
Solution:
Given, 7a + i(3a – b) = 14 – 6i
⇒ 7a + i(3a – b) = 14 + i(-6)
Now equating real and imaginary parts on both sides, we have
7a = 14 and 3a – b = -6
⇒ a = 2 and 3 ∙ 2 – b = -6
⇒ a = 2 and 6 – b = -6
⇒ a = 2 and – b = -12
⇒ a = 2 and b = 12
Therefore, the value of a = 2 and the value of b = 12.
Information Source: