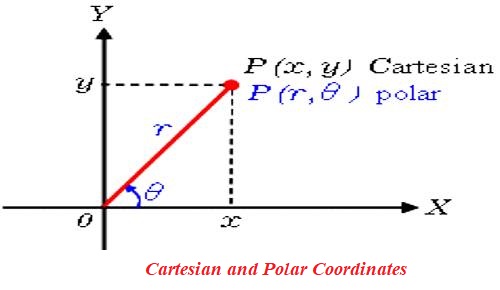
Polar Co-ordinates are widely used in higher mathematics as well as in other branches of science. In polar co-ordinate system, the position of a point on the reference plane is uniquely determined referred to a fixed point on the plane and a half line drawn through the fixed point. The fixed point is called the Pole or Origin and the half line is drawn through the pole is called the Initial Line.
Find the distance between two Points in Polar Co-ordinates
First Method: Let OX be the initial line through the pole O of the polar system and (r₁, θ ₁) and (r₂, θ₂) the polar co-ordinates of the points P and Q respectively. Then, OP₁ = r₁, OQ = r₂, ∠XOP = θ₁ and ∠XOQ = θ₂, Therefore, ∠POQ = θ₂ – θ₁.
From triangle POQ we get,
PQ² = OP² + OQ² – 2 ∙ OP ∙ OQ ∙ cos∠POQ
= r₁² + r₂² – 2r₁ r₂ cos(θ₂ – θ₁)
Therefore, PQ = √[r₁² + r₂ ² – 2r₁ r₂ cos(θ₂ – θ₁)].
Second Method: Let us choose the origin and the positive x-axis of the cartesian system as the pole and initial line respectively of the polar system. If (x₁, y₁), (x₂, y₂) and (r₁, θ₁) (r₂, θ₂) be the respective Cartesian and polar co-ordinates of the points P and Q, then we shall have,
x₁ = y₁ cos θ₁, y₁ = r₁ sin θ₁
and, x₂ = r₂ cos θ₂, y₂ = r₂ sin θ₂.
Now, the distance between the points P and Q is
PQ = √[(x₂ – x₁)² + (y₂ – y₁)²]
= √[(r₂ cos θ₂ – r₁ cos θ₁)² + (r₂ sin θ₂ – r₂ sin θ₂)²]
= √[r₂² cos² θ₂ + r₁ ² cos² θ₁ – 2 r₁r₂ cos θ₁ cos θ₂ + r₂² sin² θ₂ + r₁²sin² θ₁ – 2 r₁r₁ sin θ₁ sin θ₂]
= √[r₂² + r₁² – 2r₁ r₂ Cos(θ₂ – θ₁)].
Example on the distance between two points in polar Co-ordinates:
Find the length of the line segment joining the points (4, 10°) and (2√3 ,40°).
Solution:
We know that the length of the line segment joining the points (r₁, θ₁), and (r₂, θ₂), is
√[ r₂² + r₁² – 2r₁ r₂ Cos(θ₂ – θ₁)].
Therefore, the length of the line-segment joining the given points
= √{(4² + (2√3)² – 2 ∙ 4 ∙ 2√(3) Cos(40 ° – 10°)}
= √(16 + 12 – 16√3 ∙ √3/2)
= √(28 – 24) = √4 = 2 units.
Information Source;