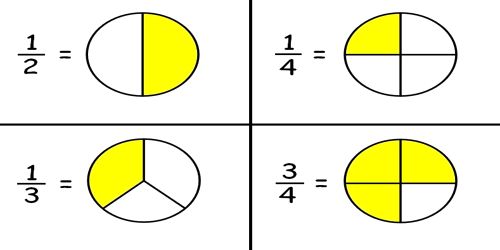
When an object is divided into a number of equal parts then each part is called a fraction. Fractions are rational numbers that are written with a numerator and a denominator. It is a numerical representation (such as ½, ¼, or 3.234) indicating the quotient of two numbers.
You can recognize a fraction by the slash that is written between the two numbers. We have a top number, the numerator, and a bottom number, the denominator. For example, 1/2 is a fraction. You can write it with a slanted slash like we have or you can write the 1 on top of the 2 with the slash between the two numbers. The 1 is the numerator, and the 2 is the denominator.
Proper and Improper Fractions
First, we have what we call ‘proper’ and ‘improper’ fractions. Proper fractions are those fractions where the numerator is less than the denominator. An improper fraction is a fraction where the numerator is greater than the denominator. For example, the fraction 7/8 is a proper fraction, where 8/7 is an improper fraction.
Here are some other important fraction terms to review:
Proper fraction: Numerator is less than the denominator. When the numerator is less than the denominator, we call the expression a proper fraction. These are some examples of proper fractions. Example: 4/3, 2/3 etc.
Improper fraction: Numerator is greater than or equal to denominator. An improper fraction occurs when the numerator is greater than or equal to the denominator. These are some examples of improper fractions: 4/3, 5/6 etc.
Mixed number: Whole number and a fraction. When an expression consists of a whole number and a proper fraction, we call it a mixed number. Here are some examples of mixed numbers: (3 x 1/3); (5 x 3/5) etc.
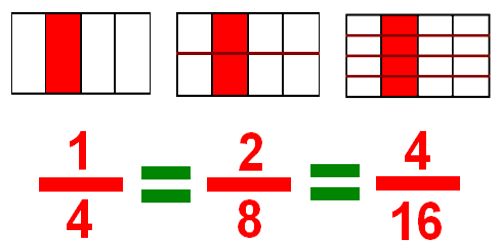
Equivalent fractions: Fractions that represent the same number. There are many ways to write a fraction of a whole. Fractions that represent the same number are called equivalent fractions. Example: ½, 2/4, 4/8 etc.
Reciprocal: the multiplicative inverse of a number. For a fraction, it’s obtained by “turning the fraction over.” When the product of two fractions equals 1, the fractions are reciprocals. Every nonzero fraction has a reciprocal.
Information Sources: