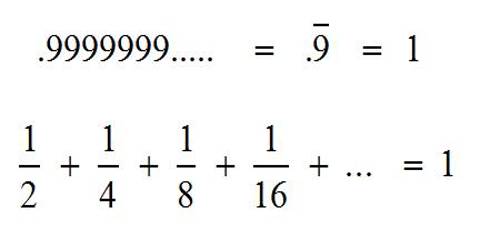Infinite Series
The power series Σxn. Binomial series (1 + x)n (n ≠ positive integer), exponential and logarithmic series with ranges of validity (statement only).
The sum of infinite terms that follow a rule. When we have an infinite sequence of values:
1/2, 1/4, 1/8, 1/16, …
which follow a rule (in this case each term is half the previous one), and we add them all up:
1/2 + 1/4 + 1/8 + 1/16 + … = S
we get an infinite series. So, it is the sum of infinitely many numbers related in a given way and listed in a given order.
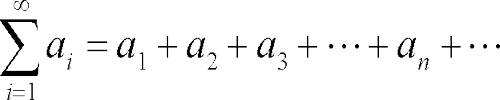
In modern terminology, any (ordered) infinite sequence (a1, a2, a3, ……) of terms (that is numbers, functions, or anything that can be added) defines a series, which is the operation of adding the ai one after the other. To emphasize that there is an infinite number of terms, a series may be called an infinite series. Such a series is represented (or denoted) by an expression like
a1 + a2 + a3 + … …
or, using the summation sign, Σ∞i=1 ai.
The infinite sequence of additions implied by a series cannot be effectively carried on (at least in a finite amount of time). However, if the set to which the terms and their finite sums belong has a notion of limit, it is sometimes possible to assign a value to a series, called the sum of the series. This value is the limit as n tends to infinity (if the limit exists) of the finite sums of the n first terms of the series, which are called the nth partial sums of the series.
An infinite series is the sum of the values in an infinite sequence of numbers. In the above examples, the sum of the numbers in N is the series n = 0 + 1 + 2 + 3 + …, which is undefined. But the sum of the numbers in S is the series s = 1 + 1/2 + 1/4 + 1/8 + … + 1/2n + …, which is defined and equal to 2. When the sum of an infinite series is finite and definable, then that series and its corresponding sequences converge. Otherwise, the series and its corresponding sequence diverge.
Information Source: