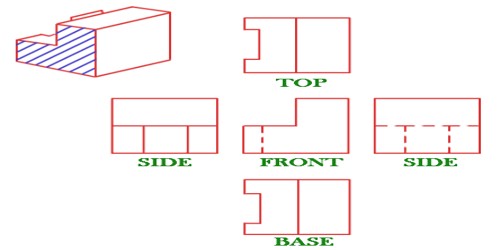
Orthogonal Projection:
A projection of a figure by parallel rays. In such a projection, tangencies are preserved. Parallel lines project to parallel lines. The ratio of lengths of parallel segments is preserved, as is the ratio of areas. Orthogonal Projection is a system of making engineering drawings showing several different views of an object at right angles to each other on a single drawing. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are not orthogonal to the projection plane.
(a) If a perpendicular is drawn from an external point on a given line then the foot of the perpendicular is called the orthogonal projection (or simply the projection) of the external point on the given line.
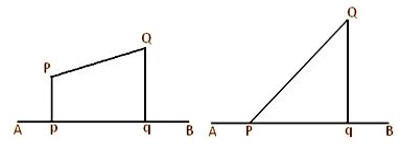
In the above-left side figure, Pp is perpendicular from the external point P on the straight line AB. Since the foot of the perpendicular is p hence, p is the projection of P on the on the line AB. Again, we can observe that in the above right side figure, 5 the point P lies on the line AB; hence, in this case, the projection of P on AB is the point P itself.
(b) The locus of the feet of the perpendiculars drawn from all points of a line (straight or curved) on a given straight line is called the projection of the line on the given straight line.
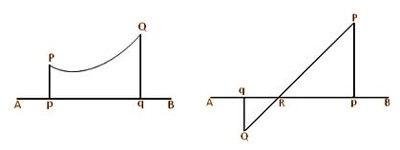
In the above-left side figure, Pp and Qq are perpendiculars from P and Q respectively on the straight line AB; p and q are the respective feet of perpendiculars. Then, pq is the projection of the straight line PQ on the straight line AB. Again, previous left-hand side figure, the projection of the straight line PQ on the straight line AB is Pq. Again, similarly, we can observe that in the above right side figure, pq is the projection of the curved line PQ on the straight line AB. Again, suppose the straight line PQ intersects the straight line AB at R; in this case, the projections of QR and RP on AB are qR and Rp respectively.
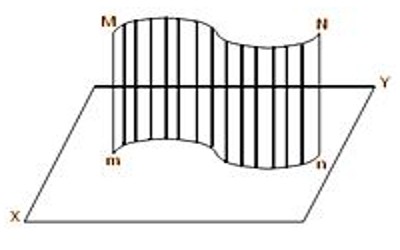
(c) The locus of the feet of the perpendiculars drawn from all points of a line (straight or curved) on a given plane is called the projection of the line on the plane. In this figure, the locus of the feet of the perpendiculars drawn from points of the line MN on the plane XY is the line mn; hence, the projection of the line MN on the plane XY is the line mn.
Note:
(i) The projection of a straight line on a plane is a straight line, but the projection of a curved line on a plane may be a straight line as well as a curved line. If the curved line MN lies in a plane which is perpendicular to the plane XY then the projection of MN on the plane XY is a straight line.
(ii) A straight line and its projection on a plane are co-planar.
Information Source: