Positive Integers are the counting numbers or natural numbers (i.e. 1, 2, 3, …).
The set of positive integers is the same as the set of natural numbers. The positive integers are the numbers 1, 2, 3, 4, … , sometimes called the natural numbers or counting numbers. Positive integers are denoted as Z+.
Z+ = {1, 2, 3, 4, ………..}
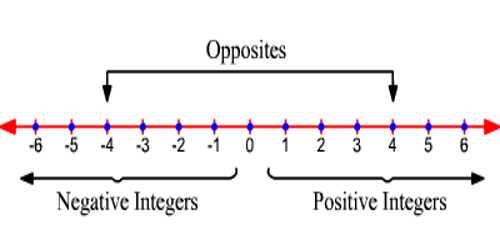
Positive integer is any whole number greater than zero, 1, 2, 3, 4, 5, 6 ………. . For each positive integer, there is a negative integer, and these integers are called opposites.
For example: Negative integer of 4 is -4.
Explanation
Positive integers are actually part of a larger group of numbers called integers. Integers are all the whole numbers, both positive and negative. By whole numbers we mean numbers without fractions or decimals. You can also call positive integers your ‘counting numbers’ because they are the same. You don’t count with fractions or decimals or negative numbers.
On a number line, positive integers are all the numbers to the right of the zero.
Positive integers are numbers you see all around you in the world. The speed limit signs posted all over our roadways are all positive integers. When you set the table for dinner, the number of plates needed is a positive integer. The same goes with the number of chairs required for family and guests. In math, positive integers are the numbers you see that aren’t fractions or decimals. They are the easy numbers.
1 346 8 78 7 485 34 98 7 225 2 6 11
All the numbers above are positive integers. Note how none of them have the negative symbol in front, nor do they have fractions or decimals. These are the numbers that are easy to work with because you don’t have to worry about the rules of fractions or decimals.
Example: Find the three consecutive positive integers whose sum is 18.
Solution:
Let x be the first positive integer. Then x + 1 and x + 2 are the other integers.
According to the statement:
x + (x + 1) + (x + 2) = 18
3x + 3 = 18
3(x + 1) = 18
x + 1 = 6
x = 5 (First integer)
Second integer = x + 1 = 5 + 1 = 6
Third integer = x + 2 = 5 + 2 = 7
∴ The three consecutive positive integers are 5, 6, 7.
Conclusion:
All integers (either positive or negative) have a counterpart that is the same distance to zero, but is on the other side of zero. This is one of the characteristics of integers, where we say that all integers have “opposite” counterparts. For example, -7 and +7 are the same distance from zero, so we say that they are opposites of each other. There is no distance between zero and itself, and it’s neither to the left nor the right of itself, so once again we say that zero is neither positive nor negative!
Information Sources: