Definitions of surds: A root of a positive real quantity is called a surd if its value cannot be exactly determined. It is a number that can’t be simplified to remove a square root (or cube root etc). For example, each of the quantities √3, ∛7, ∜19, (16)^2/5 etc. is a surd.
More Examples:
- √2 (square root of 2) can’t be simplified further so it is a surd
- √4 (square root of 4) CAN be simplified to 2, so it is NOT a surd
The surd is represented by symbol √.The symbol √ is equaled to ½. If we have a number and we are not able to obtain its root. It is called a surd. The roots of those numbers which cannot be exactly obtained.
Properties of Surds
If a and b are both rationals and √x and √y are both surds and a + √x = b + √y then a = b and x = y
If a not equal to b, let us assume, b = a + m, where m (m ≠ 0) is rational.
Now, by question, a + √x = b + √y
⇒ a + √x = a + m + √y
⇒ √x = m + √y, which is impossible (since a simple quadratic surd cannot be equal to the sum of a rational quantity and a simple quadratic surd).
Therefore, we must have, a = b.
When a = b then a + √x = b + √y ⇒ √x = √y ⇒ x = y.
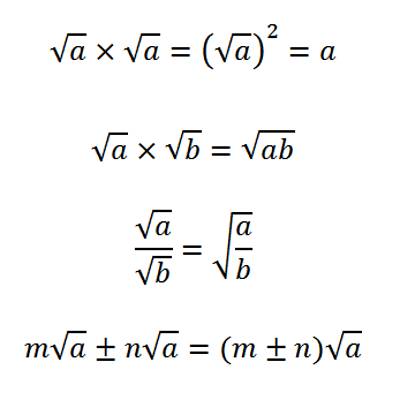
Notes:
- If a – √x = b – √y where a, b are both rationals and √x, √y are both surds, then proceeding as above we can show a = b and x = y.
- If √x and √y are actually rationals (in the form of surds), then the relation a + √x = b + √y does not imply a = b and x = y.
For example, we have,
10 = 6 + 4 = 6 + √16 and 10 = 4 + 6 = 4 + √36
⇒ 6 + √16 = 4 + √36
Evidently we cannot have, 6 = 4 or 16 = 36.
This is due to the fact that √16 and √36 are not surds, they represent rational numbers.
- If a + √x = b + √y where a, b are both rationals and √x, √y are both surds then, a = b i.e. rational parts of two sides are equal and x = y i.e., irrational parts of two sides are equal.
- If a – √x = b – √y where a, b are both rationals and √x, √y are both surds then, a = b i.e. rational parts of two sides are equal and x = y i.e., irrational parts of two sides are equal.
- If a + √x = 0, then a = 0 and x = 0.
- If a – √x = 0, then a = 0 and x = 0.
- If a + √x = b + √y then, a – √x = b – √y
- If √(a + √x) = √b + √y then √(a – √x) = √b – √y
- Identically, if √(a – √x) = √b – √y then √(a – √x) = √b – √y.
Information Source;