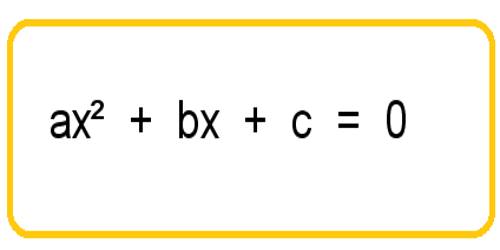A polynomial of the second degree is generally called a quadratic polynomial. In elementary algebra, the quadratic formula is the solution of the quadratic equation. There are other ways to solve the quadratic equation instead of using the quadratic formula, such as factoring, completing the square, or graphing. Using the quadratic formula is often the most convenient way.
If f(x) is a quadratic polynomial, then f(x) = 0 is called a quadratic equation.
An equation in one unknown quantity in the form ax2 + bx + c = 0 is called quadratic equation.
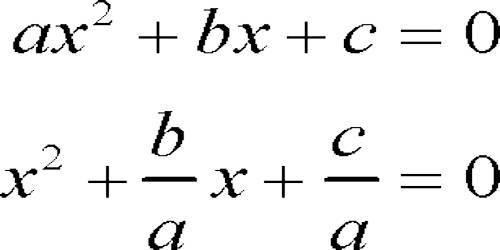
Quadratic Equation cannot have more than Two Roots
Proof:
Let us assumed that α, β and γ be three distinct roots of the quadratic equation of the general form ax2 + bx + c = 0, where a, b, c are three real numbers and a ≠ 0. Then, each one of α, β and γ will satisfy the given equation ax2 + bx + c = 0.
Therefore,
aα2 + bα + c = 0 …………… (i)
aβ2 + bβ + c = 0 …………… (ii)
aγ2 + bγ + c = 0 …………… (iii)
Subtracting (ii) from (i), we get
a(α2 – β2) + b(α – β) = 0
⇒ (α – β)[a(α + β) + b] = 0
⇒ a(α + β) + b = 0, …………… (iv) [Since, α and β are distinct, Therefore, (α – β) ≠ 0]
Similarly, Subtracting (iii) from (ii), we get
a(β2 – γ2) + b(β – γ) = 0
⇒ (β – γ)[a(β + γ) + b] = 0
⇒ a(β + γ) + b = 0, …………… (v) [Since, β and γ are distinct, Therefore, (β – γ) ≠ 0]
Again subtracting (v) from (iv), we get
a(α – γ) = 0
⇒ either a = 0 or, (α – γ) = 0
But this is not possible, because by the hypothesis a ≠ 0 and α – γ ≠ 0 since α ≠ γ
α and γ are distinct.
Thus, a(α – γ) = 0 cannot be true.
Therefore, our assumption that a quadratic equation has three distinct real roots is wrong.
Hence, every quadratic equation cannot have more than 2 roots.
Note: If a condition in the form of a quadratic equation is satisfied by more than two values of the unknown then the condition represents an identity.
Consider the quadratic equation of the general from ax2 + bx + c = 0 (a ≠ 0)
Information Source: