Reciprocal Relations of Trigonometric Ratios
Reciprocal relations of trigonometric ratios are explained here to represent the relationship between the three pairs of trigonometric ratios as well as their reciprocals.
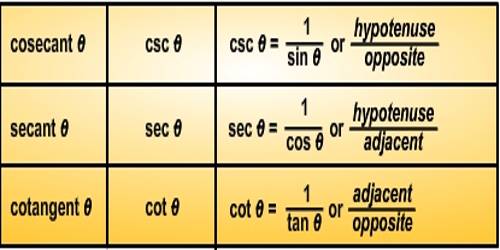
There are three reciprocal trigonometric functions, making a total of six including cosine, sine, and tangent. The reciprocal cosine function is secant: sec(theta)=1/cos(theta). The reciprocal sine function is cosecant, csc(theta)=1/sin(theta). The reciprocal tangent function is cotangent, expressed two ways: cot(theta)=1/tan(theta) or cot(theta)=cos(theta)/sin(theta).
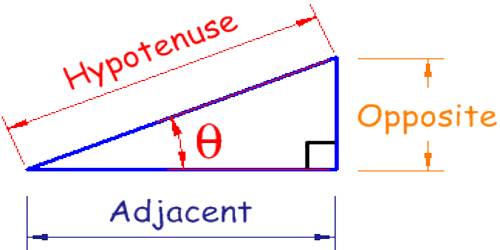
Let OMP be a right-angled triangle at M and ∠MOP = θ.
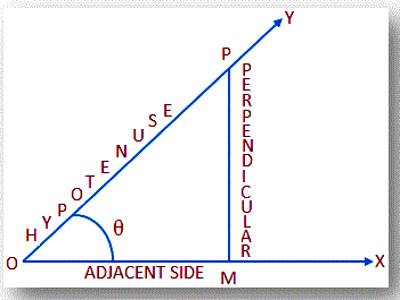
According to the definition of trigonometric ratios we have,
- sin θ = perpendicular/hypotenuse = MP/PO ………….. (i)
and csc θ = hypotenuse/perpendicular = PO/MP ………….. (ii)
From (i) sin θ = 1/(PO/MP)
⇒ sin θ = 1/csc θ ………………… (A)
Again, from (ii) csc θ = 1/(MP/PO)
⇒ csc θ = 1/sin θ ………………… (B)
From (A) and (B) we conclude that
sin θ and csc θ are reciprocal of each other.
- cos θ = adjacent/hypotenuse = OM/OP ………….. (iii)
and sec θ = hypotenuse/adjacent = OP/OM ………….. (iv)
From (iii) cos θ = 1/(OP/OM)
⇒ cos θ = 1/sec θ ………………… (C)
Again, from (iv) sec θ = 1/(OM/OP)
⇒ sec θ = 1/cos θ ………………… (D)
From (C) and (D) we conclude that
cos θ and sec θ are reciprocal of each other.
- tan θ = perpendicular/adjacent = MP/OM ………….. (v)
and cot θ = adjacent/perpendicular = OM/MP ………….. (vi)
From (v) tan θ = 1/(OM/MP)
⇒ tan θ = 1/cot θ ………………… (E)
Again, from (vi) cot θ = 1/(MP/OM)
⇒ cot θ = 1/tan θ ………………… (F)
From (E) and (F) we conclude that
tan θ and cot θ are reciprocal of each other.
To find values of trig functions we can use these reciprocal relationships to solve different types of problems.
Note: From the above discussion about the reciprocal trigonometric functions we get;
- sin θ ∙ csc θ = 1
- cos θ ∙ sec θ = 1
- tan θ ∙ cot θ = 1
Information Source: