Rectangular Cartesian Co-ordinates Geometry
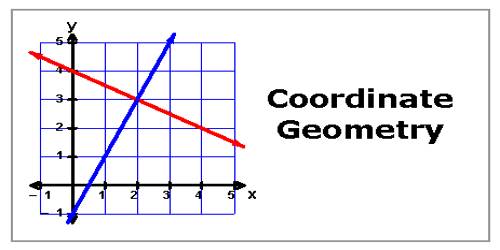
Co-ordinates Geometry is a system of geometry where the position of points on the plane is described using an ordered pair of numbers. Cartesian coordinates provide a method of rendering graphs and indicating the positions of points on a two-dimensional (2D) surface or in three-dimensional (3D) space. The two axes of two-dimensional Cartesian coordinates, conventionally denoted the x- and y-axes are chosen to be linear and mutually perpendicular.
(i) If the pole and initial line of the polar system coincides respectively with the origin and positive x-axis of the Cartesian system and (x, y), (r, θ) be the Cartesian and polar co-ordinates respectively of a point P on the plane then,
x = r cos θ, y = r sin θ
and r = √(x2 + y2), θ = tan-1(y/x).
(ii) The distance between two given points P (x1, y1) and Q (x2, y2) is PQ = √{(x2 – x1)2 + (y2 – y1)2}.
(iii) Let P (x1, y1) and Q (x2, y2) be two given points.
(a) If the point R divides the line-segment PQ internally in the ratio m : n, then the co-ordinates of R, are {(mx2 + nx1)/(m + n) , (my2 + ny1)/(m + n)}.
(b) If the point R divides the line-segment PQ externally in the ratio m : n, then the co-ordinates of R are {(mx2 – nx1)/(m – n), (my2 – ny1)/(m – n)}.
(c) If R is the mid-point of the line-segment PQ, then the co-ordinates of R are {(x1 + x2)/2, (y1 + y2)/2}.
(iv) The co-ordinates of the centroid of the triangle formed by joining the points (x1, y1) , (x2, y2) and (x3, y3) are ({x1 + x2 + x3}/3 , {y1 + y2 + y3}/3
(v) The area of a triangle formed by joining the points (x1, y1), (x2, y2) and (x3, y3) is
½ | y1 (x2 – x3) + y2 (x3 – x1) + y3 (x1 – x2) | sq. units
or, ½ | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) | sq. units.
Information Source;