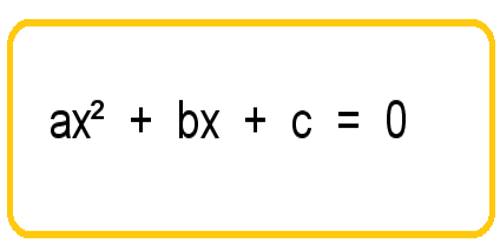Structural induction is used to prove which some proposition P(x) holds for those x of some form of recursively defined structure for instance lists or trees and shrubs. A well-founded just a few order is defined about the structures. The structural induction proof is a proof that your proposition holds for all the minimal structures, which if it holds for that immediate substructures of an certain structure Ersus, then it must hold for S also.
Structural Induction