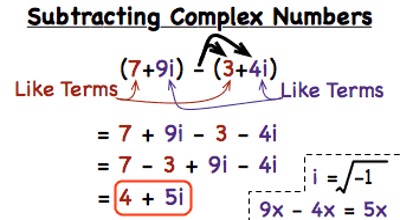
Subtraction of Complex Numbers
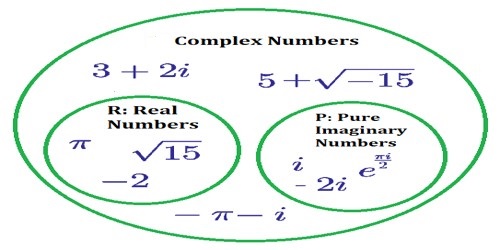
A complex number is a number of the form a + bi, where ‘a’ and ‘b’ are real numbers and ‘I’ is an indeterminate satisfying i2 = −1. For example, 2 + 3i is a complex number.
The equations x2 + 5 = 0, x2 + 10 = 0, x2 = -1 are not solvable in the real number system i.e, these equations has no real roots. For example, i is the solution of the equation x2 = -1 and it has two solutions i.e., x = ± i, where √-1.
The number, ‘I’ is called an imaginary number. Generally, the square root of any negative real number is called imaginary number. The concept of imaginary numbers was first introduced by mathematician “Euler”. He was the one who introduced ‘i’ (read as ‘iota’) to represent √-1. He also defined i2 = -1.
Here discuss the usual mathematical operation – subtraction of two complex numbers.
Subtract Complex Numbers
Let z1 = p + iq and z2 = r + is be any two complex numbers, then the subtraction of z2 from z1 is defined as
z1 – z2 = z1 + (-z2)
= (p + iq) + (-r – is)
= (p – r) + i(q – s)
The following steps of subtraction of complex numbers are given below:
Step I: Distribute the negative
Step II: Group the real part of the complex number and the imaginary part of the complex number.
Step III: Combine the like terms and simplify
For example, let z1 = 6 + 4i and z2 = -7 + 5i, then
z1 – z2 = (6 + 4i) – (-7 + 5i)
= (6 + 4i) + (7 – 5i), [Distributing the negative sign]
= (6 + 7) + (4 – 5)i, [Grouping the real part of the complex number and the imaginary part of the complex number.]
= 13 – i, [Combining the like terms and simplify]
and z2 – z1 = (-7 + 5i) – (6 + 4i)
= (-7 + 5i) + (-6 – 4i), [Distributing the negative sign]
= (-7 – 6) + (5 – 4)i, [Grouping the real part of the complex number and the imaginary part of the complex number.]
= -13 + i
Solved examples of subtraction of complex numbers:
- Find the difference between the complex numbers (2 + 3i) from (-9 – 2i).
Solution:
(-9 – 2i) – (2 + 3i)
= (-9 – 2i) + (-2 – 3i), [Distributing the negative sign]
= (- 9 – 2) + (-2 – 3)i, [Grouping the real part of the complex number and the imaginary part of the complex number.]
= -11 – 5i
- Evaluate: (7√5 + 3i) – (√5 – 2i)
Solution:
(7√5 + 3i) – (√5 – 2i)
= (7√5 + 3i) + (-√5 + 2i), [Distributing the negative sign]
= (7√5 – √5) + (3 + 2)i, [Grouping the real part of the complex number and the imaginary part of the complex number.]
= 6√5 + 5i
- Express the complex number (8 – 3i) – (-6 + 2i) in the standard form a + ib.
Solution:
(8 – 3i) – (-6 + 2i)
= (8 – 3i) + (6 – 2i), [Distributing the negative sign]
= (8 + 6) + (-3 – 2)i, [Grouping the real part of the complex number and the imaginary part of the complex number.]
= 14 – 5i, which is the required form.
Note: The final answer of Subtraction of complex numbers must be in simplest or standard form a + ib.
Information Source: