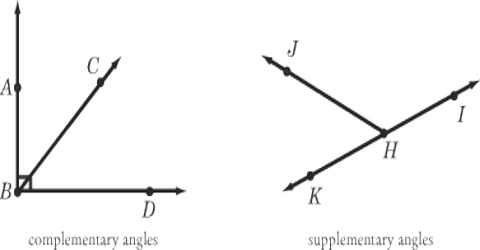
Complementary angles:
Two Angles are Complementary when they add up to 90 degrees (a Right Angle). They don’t have to be next to each other, just so long as the total is 90 degrees.
Complementary comes from Latin completum meaning “completed”, because the right angle is thought of as being a complete angle.
Examples:
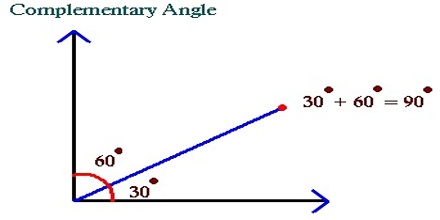
60° and 30° are complementary angles.
5° and 85° are complementary angles.
Supplementary angles:
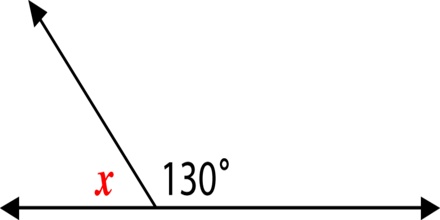
Two Angles are Supplementary when they add up to 180 degrees. If one angle is known, its supplementary angle can be found by subtracting the measure of its angle from 1800.
Example: What is the supplementary angle of 1430?
Solution: 1800 – 1430 = 370
Brief Example:
Two angles are supplementary. If the measure of the angle is twice the measure of the other, find the measure of each angle.
Let the measure of one of the supplementary angles be a.
Measure of the other angle is 2 times a.
So, measure of the other angle is 2a.
If the sum of the measures of two angles is 180°, then the angles are supplementary.
So, a+2a=180°
Simplify.
3a=180