Surface Area of Cylinders
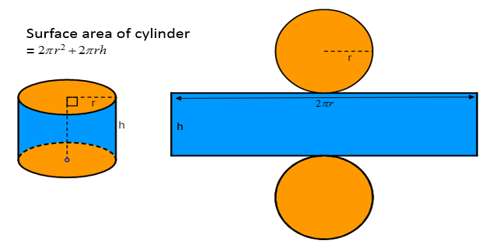
The number of square units it takes to exactly cover the surface of a cylinder. To find the surface area of a cylinder adds the surface area of each end plus the surface area of the side. Each end is a circle so the surface area of each end is π * r2, where r is the radius of the end. There are two ends so their combinded surface area is 2 π * r2. The surface area of the side is the circumference times the height or 2 π * r * h, where r is the radius and h is the height of the side.
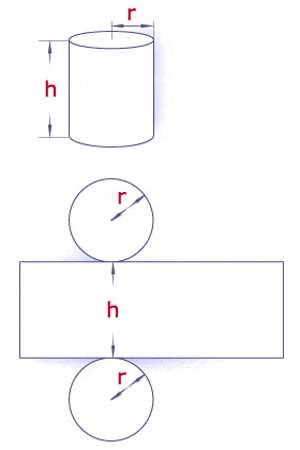
The surface area of a cylinder can be found by breaking it down into three parts:
- The two circles that make up the ends of the cylinder.
- The side of the cylinder, which when “unrolled” is a rectangle
The entire formula for the surface area of a cylinder is- (2 π r2 + 2 π r h)
h = height of the cylinder, r = radius of the top, approximate value of pi: 3.14.
Similar to the rectangle we just finished,
Surface Area = Areas of top and bottom + Area of the side(s)
Unlike the rectangle, which has 4 sides, the cylinder only has 1 side.
Let’s picture our cylinder-shaped gift. The surface area is the areas of all the parts needed to cover the can, which are the top and bottom circles and the rectangular paper label that folds around the middle.
Circle area formula is π r2. Since there is both a top and a bottom, that gets multiplied by two.
Let’s use another example, a soup can. The side is like the paper label of a soup can. When you peel it off and lay it flat, it will be a rectangle. The area of a rectangle is the product of the two sides. One side is the height of the can, the other side is the perimeter of the circle, also known as the circumference of a circle. Since the label wraps once around the can, the area of the rectangle is the circumference of the circle x height or (2 π r) * h.
Information Source: