Theorem of Three Perpendiculars
A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a first line is perpendicular to a second line if (1) the two lines meet, and (2) at the point of intersection the straight angle on one side of the first line is cut by the second line into two congruent angles.
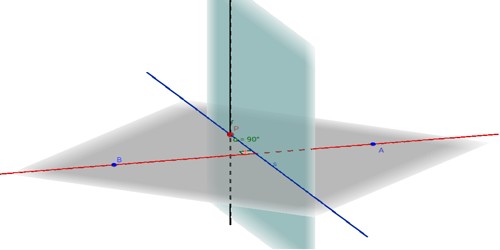
Theorem: If PQ is perpendicular to a plane XY and if from Q, the foot of the perpendicular, a straight line QR is drawn perpendicular to any straight line ST in the plane, then PR is also perpendicular to ST.
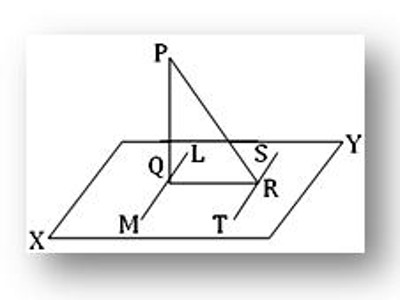
Construction: Through Q draw in the plane XY the straight line LM parallel to ST.
Proof: Since LM is parallel to ST and QR perpendicular to ST hence, QR is perpendicular to LM. Again, PQ is perpendicular to the plane XY; hence, it is perpendicular to the line LM. Therefore, LM is perpendicular to both PQ and QR at Q. This implies LM is perpendicular to the plane PQR. Now, ST and LM are parallel and LM is perpendicular to the plane PQR; hence, ST is perpendicular to the plane PQR. Therefore, ST is perpendicular to PR or in other words, PR is perpendicular to ST.
Example: Straight lines in space which are parallel to a given straight line are parallel to one another.
Let AB and CD be two straight lines each of which is parallel to the given line LM. We are to prove that the straight lines AB and CD are parallel to each other.
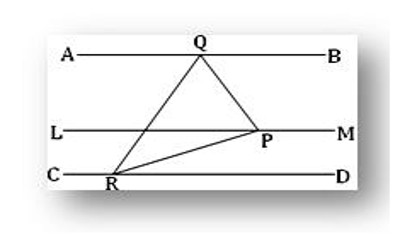
Construction: Draw a plane PQR perpendicular to LM and let us assume that the drawn plane cuts LM, AB and CD at P, Q, and R respectively.
Proof: By hypothesis, AB is parallel to LM and by construction, LM is perpendicular to the plane PQR. Therefore, AB is also perpendicular to the plane PQR. Similarly, CD is also perpendicular to the same plane. Thus, each of AB and CD is perpendicular to the same plane PQR. Therefore, the straight lines AB and CD are parallel to one another.
Information Source: