Volume of a Pyramid
The volume of a 3-dimensional solid is the amount of space it occupies. Volume is measured in cubic units ( in3, ft3, cm3, m3 etcetera). The volume enclosed by a pyramid is one third of the base area times the perpendicular height.
A pyramid is any shape that goes up to a point at the top. The base can be any shape, but when the base is a circle it is called a cone.
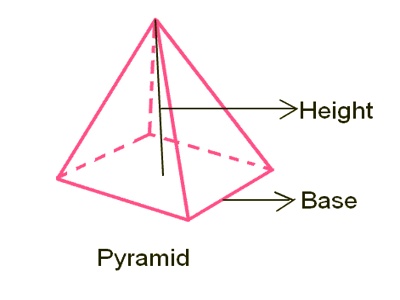
A pyramid has a base and triangular sides which rise to meet at the same point. The base may be any polygon such as a square, rectangle, triangle, etc. The general formula for the volume of a pyramid is:
Volume = Area of the base x Height x 1/3 = 1/3 ah
where, ‘a’ is the area of the base and h is the height of the pyramid.
The volume of a pyramid with a rectangular base is equal to:
Volume: Length of base x Width of base x Height x 1/3
Example:
A pyramid has a square base of side 4 cm and a height of 9 cm. Find its volume.
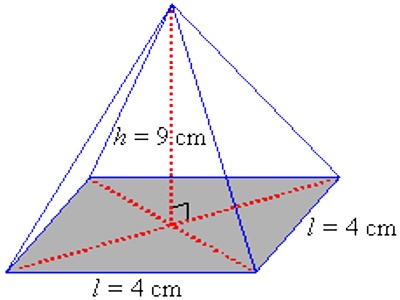
Solution:
V = 1/3 ah
= 1/3 l2h
= 1/3 (42 x 9) = 48