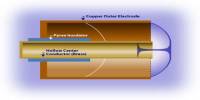
About Magnetohydrodynamics (MHD)
Definition
Magnetohydrodynamics or MHD, also known as magnetofluid mechanics, or hydromagnetics, the description of the behaviour of a plasma, or, in general, any electrically conducting fluid in the presence of electric and magnetic fields.
The word “magnetohydrodynamics” is derived from magneto- meaning magnetic field, hydro- meaning water, and -dynamics meaning movement. The field of MHD was initiated by Hannes Alfvén, for which he received the Nobel Prize in Physics in 1970.
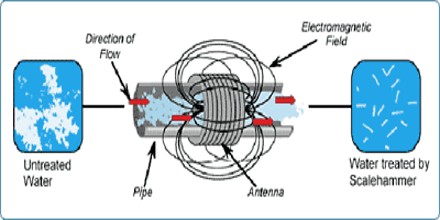
It is a branch of the science of the dynamics of matter moving in an electromagnetic field, especially where currents established in the matter by induction modify the field, so that the field and dynamics equations are coupled. It treats, in particular, conducting fluids, whether liquid or gaseous, in which certain simplifying postulates are accepted. These are, generally, that the Maxwell displacement current is neglected, and the fluid may be treated as a continuum, without mean-free-path effects. It is distinguished from the closely related plasma dynamics in which these postulates are relaxed, but there is still a large intermediate area in which similar treatment is possible.
MHD was originally applied to astrophysical and geophysical problems, where it is still very important, but more recently to the problem of fusion power, where the application is the creation and containment of hot plasmas by electromagnetic forces, since material walls would be destroyed. Astrophysical problems include solar structure, especially in the outer layers, the solar wind bathing the earth and other planets, and interstellar magnetic fields. The primary geophysical problem is planetary magnetism, produced by currents deep in the planet, a problem that has not been solved to any degree of satisfaction.
Principles of Magnetohydrodynamics
The theoretical dynamical properties of magnetic fields and plasmas are introduced with a review of the motion of an individual charged particle moving freely in a large-scale non-uniform magnetic field, including the adiabatic invariants of the motions, mirroring, etc. The velocity moments of the collisional Boltzmann equation are developed in the conventional manner to obtain the partial differential equations for conservation of particles and momentum density, followed by the energy equation and the coefficients of thermal conductivity, viscosity, and resistivity. The magnetic dissipation term is constructed using the scalar form of Ohm’s law, and MHD follows with the tacit assumption that the system is not overwhelmed by resistive dissipation. And here it should be understood that the essential feature of MHD is that the magnetic field is carried bodily with the bulk motion of the plasma in the limit of vanishing resistivity.
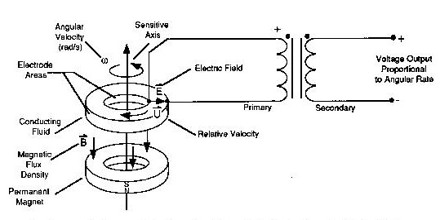
The MHD equations are subsequently cast in conservation form, in terms of entropy p/ργ , thermal energy density, etc. with clear emphasis on the stresses in the magnetic field and their central role in the dynamical interplay with the pressure and inertia of the moving plasma.
Use of MHD is unavoidable for the large-scale bulk dynamics of a fluid containing a sufficient number of free electrons and ions. There are two necessary and sufficient conditions. First, the large-scale dynamics of any gas with a number density large enough to give an accurate statistical definition of the local gas density is described by the familiar hydrodynamic momentum equation, with the pressure tensor understood to represent the momentum flux density in the thermal motions. Second, if there are enough free electrons and ions that the sufficiently dense fluid cannot support any significant electric field in its own moving frame of reference, then the magnetic field is carried bodily with the fluid, and the large-scale bulk gas dynamics automatically becomes MHD.
Ideal MHD Equations
The ideal MHD equations consist of the continuity equation, the Cauchy momentum equation, Ampere’s Law neglecting displacement current, and a temperature evolution equation. As with any fluid description to a kinetic system, a closure approximation must be applied to highest moment of the particle distribution equation. This is often accomplished with approximations to the heat flux through a condition of adiabaticity or isothermality.

Ideal MHD is only strictly applicable when:
The plasma is strongly collisional, so that the time scale of collisions is shorter than the other characteristic times in the system, and the particle distributions are therefore close to Maxwellian.
The resistivity due to these collisions is small. In particular, the typical magnetic diffusion times over any scale length present in the system must be longer than any time scale of interest.
Interest in length scales much longer than the ion skin depth and Larmor radius perpendicular to the field, long enough along the field to ignore Landau damping, and time scales much longer than the ion gyration time, system is smooth and slowly evolving.