Antiferromagnetism in Physics
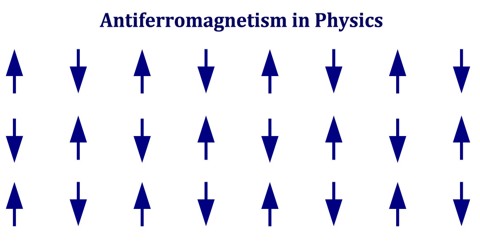
Antiferromagnetism means that the electrons within the material do not align themselves with the same magnetic polarity. Even within the specific domains, the material does not display any magnetic qualities. As a result of the electrons not aligning themselves in the same polarity, they cancel each other out with the specific chain of electrons. This is different from ferromagnetism, because in ferromagnetic materials, the chains consist of electrons with matching polarity, but the different chains cancel each other out. The name antiferromagnetism is derived from the opposite term, ferromagnetism.

Antiferromagnetism is the opposite of ferromagnetism, where particles align themselves, and occurs in materials such as manganese oxide. The phenomenon generally decreases as the temperature rises, the electrons scattering arbitrarily and no longer forming chains. The temperature at which this occurs is referred to as the Neel temperature.
Antiferromagnetism, type of magnetism in solids such as manganese oxide (MnO) in which adjacent ions that behave as tiny magnets (in this case manganese ions, Mn2+) spontaneously align themselves at relatively low temperatures into opposite, or antiparallel, arrangements throughout the material so that it exhibits almost no gross external magnetism. In antiferromagnetic materials, which include certain metals and alloys in addition to some ionic solids, the magnetism from magnetic atoms or ions oriented in one direction is canceled out by the set of magnetic atoms or ions that are aligned in the reverse direction.
Examples of Antiferromagnetic Materials
Antiferromagnetic materials occur commonly among transition metal compounds, especially oxides. Examples include hematite, metals such as chromium, alloys such as iron manganese (FeMn), and oxides such as nickel oxide (NiO). There are also numerous examples among high nuclearity metal clusters. Organic molecules can also exhibit antiferromagnetic coupling under rare circumstances, as seen in radicals such as 5-dehydro-m-xylylene.
In the presence of the strong magnetic field, antiferromagnetic materials are weakly magnetised in the direction the field. This property of the materials is called antiferromagnetism and the materials which exhibit this propert are called antiferromagnetic materials.
Examples of antiferromagnetic substances: MnO, FeO, CoO, NiO, Cr, Mn, MnO4, MnS, FeCl3, MnF2
Measurement of Antiferromagnetism
Measurements of magnetic noise emanating from ferromagnets owing to domain motion were first carried out nearly 100 years ago, and have underpinned much science and technology. Antiferromagnets, which carry no net external magnetic dipole moment, yet have a periodic arrangement of the electron spins extending over macroscopic distances, should also display magnetic noise.
The magnetic susceptibility of an antiferromagnetic material typically shows a maximum at the Néel temperature. In contrast, at the transition between the ferromagnetic to the paramagnetic phases the susceptibility will diverge. In the antiferromagnetic case, a divergence is observed in the staggered susceptibility.
Various microscopic (exchange) interactions between the magnetic moments or spins may lead to antiferromagnetic structures. In the simplest case, one may consider an Ising model on a bipartite lattice, e.g. the simple cubic lattice, with couplings between spins at nearest neighbor sites. Depending on the sign of that interaction, ferromagnetic or antiferromagnetic order will result. Geometrical frustration or competing ferro- and antiferromagnetic interactions may lead to different and, perhaps, more complicated magnetic structures.
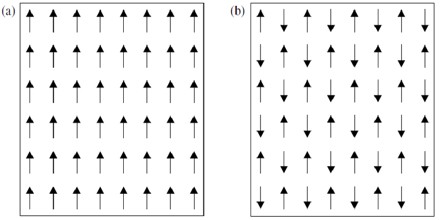
Geometric Frustration
Unlike ferromagnetism, anti-ferromagnetic interactions can lead to multiple optimal states. In one dimension, the anti-ferromagnetic ground state is an alternating series of spins: up, down, up, down, etc. Yet in two dimensions, multiple ground states can occur.
Consider an equilateral triangle with three spins, one on each vertex. If each spin can take on only two values (up or down), there are 23 = 8 possible states of the system, six of which are ground states. The two situations which are not ground states are when all three spins are up or are all down. In any of the other six states, there will be two favorable interactions and one unfavorable one. This illustrates frustration: the inability of the system to find a single ground state. This type of magnetic behavior has been found in minerals that have a crystal stacking structure such as a Kagome lattice or hexagonal lattice.
There are also examples of disordered materials, such as iron phosphate glasses that become antiferromagnetic below their Néel temperature. These disordered networks ‘frustrate’ the antiparallelism of adjacent spins; i.e. it is not possible to construct a network where each spin is surrounded by opposite neighbour spins. It can only be determined that the average correlation of neighbour spins is antiferromagnetic. This type of magnetism is sometimes called speromagnetism.