Definition of Nuclear Shell Model
Nuclear Shell Model is partly analogous to the atomic shell model which describes the arrangement of electrons in an atom, in that a filled shell results in greater stability. It is a model of the atomic nucleus which uses the Pauli Exclusion Principle to describe the structure of the nucleus in terms of energy levels.
In order to describe the internal workings of the nucleus, three nuclear structure models have been proposed, including the Liquid-Drop Model, first proposed in the 1940s by the Danish physicist, Niels Bohr, the Nuclear Shell Model, proposed independently by Maria Goeppert Mayer and Johannes H. D. Jenson in 1949, and the Collective Model, a variation on the liquid-drop idea. Many of the theories of nuclear physics use all three models in order to describe various and diverse phenomenon. As such, the three theories have a commonality not unlike the wave-particle duality of electromagnetism.
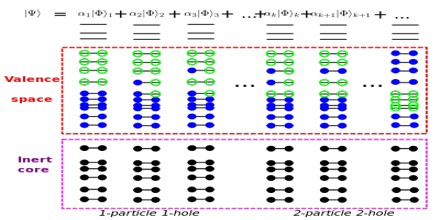
The model was developed in 1949 following independent work by several physicists, most notably Eugene Paul Wigner, Maria Goeppert Mayer and J. Hans D. Jensen, who shared the 1963 Nobel Prize in Physics for their contributions.
According to this model, the motion of each nucleon is governed by the average attractive force of all the other nucleons. The resulting orbits form “shells,” just as the orbits of electrons in atoms do. As nucleons are added to the nucleus, they drop into the lowest-energy shells permitted by the Pauli Principle which requires that each nucleon have a unique set of quantum numbers to describe its motion.
Magic Numbers
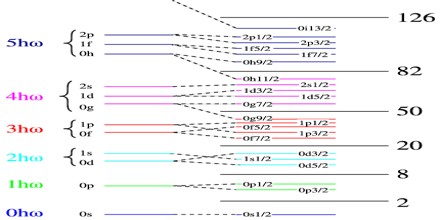
The shells for protons and for neutrons are independent of each other. Therefore, one can have “magic nuclei” where one nucleon type or the other is at a magic number, and “doubly magic nuclei”, where both are. Due to some variations in orbital filling, the upper magic numbers are 126 and, speculatively, 184 for neutrons but only 114 for protons, playing a role in the search for the so-called island of stability. Some semimagic numbers have been found, notably Z=40 giving nuclear shell filling for the various elements; 16 may also be a magic number. The binding energies predicted by the Liquid Drop Model underestimate the actual binding energies of “magic nuclei” for which either the number of neutrons N = (A − Z) or the number of protons, Z is equal to one of the following “magic numbers”
2, 8, 20, 28, 50, 82, 126
This is particularly the case for “doubly magic” nuclei in which both the number of neutrons and the number of protons are equal to magic numbers.
These magic numbers can be explained in terms of the Shell Model of the nucleus, which considers each nucleon to be moving in some potential and classifies the energy levels in terms of quantum numbers nl j, in the same way as the wavefunctions of individual electrons are classified in Atomic Physics.
Nuclear Shell Structure
The empirical relations suggest the addition of a central depression to the well for light nuclei (N or Z≦20) and a central elevation (Elsasser’s wine bottle potential) for heavy nuclei. The qualitative physical explanation of these modifications is that for light nuclei, the particle density, and thus the nuclear interaction energy, is greatest at the center of the nucleus; for heavy nuclei, the Coulomb repulsion between protons produces a particle density varying from a minimum at the center to a maximum near the boundary, and therefore a similarly varying interaction energy.
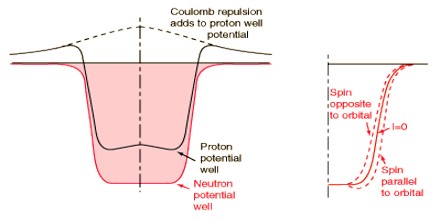
Experimentally known spins, magnetic moments and quadrupole moments of nuclei with a small number of particles outside of closed shells, or missing from closed shells, tend to corroborate the model. The agreement is particularly good for odd nuclei with one kind of nucleon forming a closed shell±one particle (and still better if the even group of nucleons constitutes a closed shell). Under these conditions, the orbit of the odd particle, as given by the shell model, usually determines the state of the nucleus, which is checked for consistency with the known spins and moments. In some cases, the reasoning is reversed as a means of fixing the crossover points between energy levels in the theory.
It is generally believed that nuclei are composed of protons and neutrons, although there is some question as to whether a nucleus contains protons and neutrons as separate substructures. It could be that a nucleus is just a bag of the quarks that compose the protons and neutrons. At one time some thought that a nucleus was composed of substructures of alpha particles (helium nuclie). For the analysis here a nucleus is considered as being composed of protons and neutrons.
However, unlike Atomic Physics, it is also possible that sometimes it is energetically cheaper to promote a nucleon from an inner closed shell, rather than a nucleon form an outer shell into a high energy state. Moreover, an excited state in which more than one nucleon is promoted above its ground state is much more common in Nuclear Physics than in Atomic Physics.
Thus the nuclear spectrum of states is very rich indeed, but very complicated and cannot be easily understood in terms of the shell model.