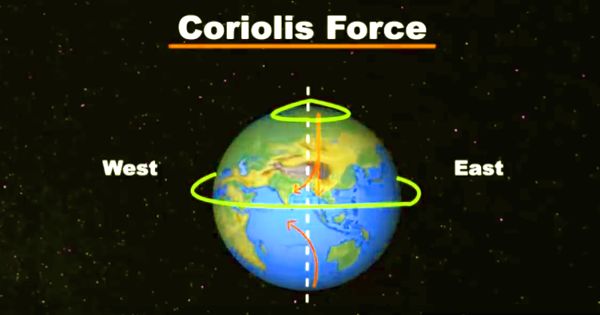
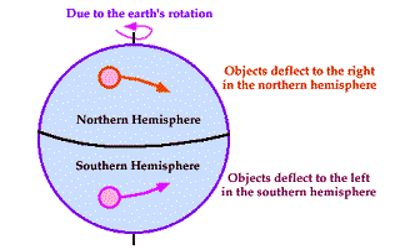
The Coriolis force acts in a direction perpendicular to Earth’s rotational axis. In physics, the Coriolis force is an inertial or fictitious force that acts on objects that are in motion within a frame of reference that rotates with respect to an inertial frame. The effect of the Coriolis force is an apparent deflection of the path of an object that moves within a rotating coordinate system. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. The magnitude of the Coriolis force depends on the speed of the object and its latitude. In one with anticlockwise (or counterclockwise) rotation, the force acts to the right. The Coriolis force is zero at the equator and increases toward the poles.
In physics, the Coriolis force is an inertial or fictitious force that acts on objects that are in motion within a frame of reference that rotates with respect to an inertial frame.
Deflection of an object due to the Coriolis force is called the Coriolis effect. The Coriolis effect is most apparent in the path of an object moving longitudinally. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. On Earth, an object that moves along a north-south path, or longitudinal line, will undergo apparent deflection to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. The Coriolis deflection is therefore related to the motion of the object, the motion of Earth, and the latitude. The impact of the Coriolis effect is most significant with high speeds or long distances. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.
Newton’s laws of motion describe the motion of an object in an inertial (non-accelerating) frame of reference. It is also significant in the earth sciences, especially meteorology, physical geology, and oceanography, in that Earth is a rotating frame of reference, and motions over the surface of Earth are subject to acceleration from the force indicated. When Newton’s laws are transformed into a rotating frame of reference, the Coriolis and centrifugal accelerations appear. When applied to massive objects, the respective forces are proportional to the masses of them.
The centrifugal force acts outwards in the radial direction and is proportional to the distance of the body from the axis of the rotating frame. The Coriolis effect describes the pattern of deflection taken by objects not firmly connected to the ground as they travel long distances around Earth. These additional forces are termed inertial forces, fictitious forces, or pseudo forces. It is responsible for many large-scale weather patterns. By accounting for the rotation by addition of these fictitious forces, Newton’s laws of motion can be applied to a rotating system as though it was an inertial system. Earth completes one rotation per day, so for everyday motions, like throwing a ball or an apple falling from a tree, the Coriolis force is very small compared to other forces and is negligible. They are correction factors which are not required in a non-rotating system. Its effects become noticeable only for motions occurring over large distances and long periods of time.