Magnetic Flux
Definition
Magnetic Flux is a measure of the strength of a magnetic field over a given area perpendicular to it, equal to the product of the area and the magnetic flux density through it. It is a useful tool for helping describe the effects of the magnetic force on something occupying a given area. The measurement of magnetic flux is tied to the particular area chosen.
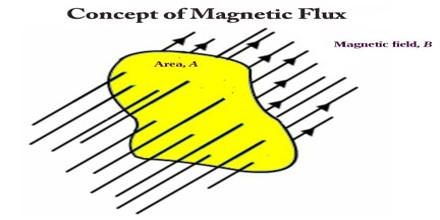
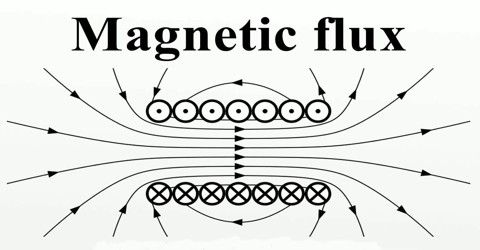
Magnetic interaction is described in terms of a vector field, where each point in space and time, which is associated with a vector that determines what force a moving charge would experience at that point. The magnetic flux through some surface, in this simplified picture, is proportional to the number of field lines passing through that surface in some contexts, the flux may be defined to be precisely the number of field lines passing through that surface; although technically misleading, this distinction is not important. Note that the magnetic flux is the net number of field lines passing through that surface; that is, the number passing through in one direction minus the number passing through in the other direction. The field line analogy is dropped and the magnetic flux is properly defined as the surface integral of the normal component of the magnetic field passing through a surface.
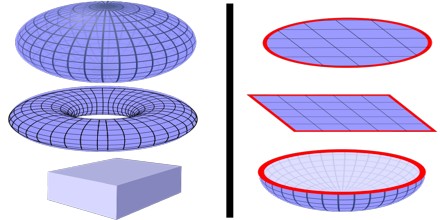
Magnetic Flux is Zero in Closed Surface
Magnetic flux through a surface is zero because, in simple words, all the field lines that enter the surface exit it.
In electrostatics there are charges that that can be enclosed by a surface, due to which there’s an electric field though the surface which leads to an electric flux. But in magnetism, there are no magnetic charges. Fundamentally, only a magnetic moment is existent, not a magnetic charge.
Gauss’s law for magnetism, which is one of the four Maxwell’s equations, states that the total magnetic flux through a closed surface is equal to zero. A “closed surface” is a surface that completely encloses a volume(s) with no holes. This law is a consequence of the empirical observation that magnetic monopoles have never been found.
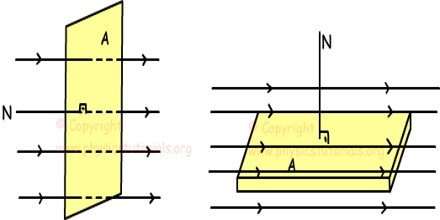
Illustrations of Magnetic Flux
The contribution to magnetic flux for a given area is equal to the area times the component of magnetic field perpendicular to the area. For a closed surface, the sum of magnetic flux is always equal to zero (Gauss’ law for magnetism). No matter how small the volume, the magnetic sources are always dipole sources (like miniature bar magnets), so that there are as many magnetic field lines coming in (to the South Pole) as out.