Biography of Daniel Bernoulli
Daniel Bernoulli – Swiss mathematician and physicist.
Name: Daniel Bernoulli
Date of Birth: 8 November 1700
Place of Birth: Groningen, Dutch Republic
Date of Death: 17 March 1782 (aged 81)
Place of Death: Basel, Republic of the Swiss
Occupation: Mathematician, Physicist
Father: Johann Bernoulli
Mother:
Spouse/Ex:
Children:
Early Life

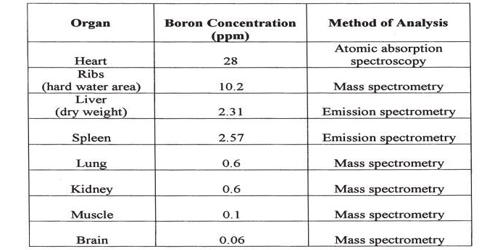
A Swiss mathematician and physicist who did pioneering work in the field of fluid dynamics and kinetic theory of gases, Daniel Bernoulli was born on 8 November 1700 in Groningen, in the Netherlands, into a family of distinguished mathematicians. He investigated not only mathematics but also such fields as medicine, biology, physiology, mechanics, physics, astronomy, and oceanography. Bernoulli’s theorem (q.v.), which he derived, is named after him.
Born in a distinguished family of mathematicians, Daniel was encouraged by his father to pursue a business career. After obtaining his Master of Arts degree, he studied medicine and was also privately tutored in mathematics by his father. Subsequently, he made a name for himself and was called to St. Petersburg, where he spent several fruitful years teaching mathematics. During this time, he wrote important texts on the theory of mechanics, including the first version of his famous treatise on hydrodynamics. Later, he served as a professor of anatomy and botany in Basel before being appointed to the chair of physics. There he taught physics for the next 26 years and also produced several other excellent scientific works during his term. In one of his most remarkable works ‘Hydrodynamica’ which was a milestone in the theory of the flowing behavior of liquids, he developed the theory of watermills, windmills, water pumps, and water propellers.
Daniel is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics. His name is commemorated in the Bernoulli’s principle, a particular example of the conservation of energy, which describes the mathematics of the mechanism underlying the operation of two important technologies of the 20th century: the carburetor and the airplane wing.
Childhood, Family and Educational Life
Daniel Bernoulli, a famous Swiss mathematician, and physicist were born on February 8, 1700, in Groningen, Netherlands, to Johann Bernoulli, a mathematician who was one of the early developers of calculus. He had two brothers, Nicolaus Bernoulli II, and Johann Bernoulli II. The Bernoulli family came originally from Antwerp, at that time in the Spanish Netherlands, but emigrated to escape the Spanish persecution of the Protestants. After a brief period in Frankfurt, the family moved to Basel, in Switzerland.
Daniel wanted to become a mathematician but his father encouraged him to pursue a business career. At the age of 13, his father sent him to Basel University to study philosophy and logic. In 1715, he completed his graduation and a year later obtained his Master’s degree. After that, upon his father’s wishes, he agreed to study medicine on the condition that his father would teach him mathematics privately. Daniel studied medicine in Basel, Heidelberg, and Strasbourg, and earned a doctorate in anatomy and botany in 1721.
However, while he was there he continued to study mathematics, publishing a book called Mathematical Exercises in 1724. In Venice, Daniel Bernoulli also invented a new type of hourglass that could be used to tell time on a ship. This was particularly challenging because of the motion of the sea, and Bernoulli’s work was recognized when he won a prize from the Paris Academy in 1725.
Personal Life
Daniel Bernoulli shared the 1735 prize for work on planetary orbits with his father, who, it is said, threw him out of the house for thus obtaining a prize he felt should be his alone. Daniel’s prizewinning papers reflected his success on the research frontiers of science and his ability to set forth clearly before an interested public the scientific problems of the day.
Career and Works

In 1724, Daniel Bernoulli left for St. Petersburg. He went there to fill a post as professor of mathematics. However, he was very unhappy and illness in 1733 gave him a reason to leave. He went back to the University of Basel where he became the chair of metaphysics, natural philosophy, and medicine. He remained here until his death. Daniel was elected a Fellow of Royal Society in the year 1750.
In 1723-24 Daniel wrote ‘Exercitationes quaedam Mathematicae’ on differential equations and the physics of flowing water, which won him a position at the influential Academy of Sciences in St. Petersburg, Russia. Bernoulli lectured there until 1732 in medicine, mechanics, and physics, and he researched the properties of vibrating and rotating bodies and contributed to probability theory. In that same year, he returned to the University of Basel to accept the post in anatomy and botany. By then he was widely esteemed by scholars and also admired by the public throughout Europe.
In 1727, a young man named Leonard Euler, who had been a student of Bernoulli’s father in Basel, came to St. Petersburg. For the next few years, Euler and Bernoulli would work together, making many discoveries that revolutionized the world of science and mathematics.
In 1732, Daniel Bernoulli became a professor of botany and anatomy at the University of Basel and later, accepted a post in physiology in 1743. His reputation was established in 1738 with Hydrodynamica, in which he considered the properties of basic importance in fluid flow, particularly pressure, density, and velocity, and set forth their fundamental relationship. He put forward what is called Bernoulli’s principle, which states that the pressure in a fluid decreases as its velocity increases. Daniel also established the basis for the kinetic theory of gases and heat by demonstrating that the impact of molecules on a surface would explain pressure and that, assuming the constant, random motion of molecules, pressure and motion increase with temperature. About 1738 his father published Hydraulica; this attempt by Johann to obtain priority for himself was another instance of his antagonism toward his son.
Daniel also wrote several papers containing mechanical questions about the vibration of strings and the works of Brook Taylor. Daniel Bernoulli also made discoveries on the motion of fluids. He made a significant discovery on the connection between the speed of the flow of blood and pressure. He performed an experiment in which he set up an apparatus that showed the relation between the two values.
Subsequently, Daniel came out with his most important work called ‘Bernoulli’s principle’, which states that the pressure in a fluid decreases as its velocity increases. In 1750, after being appointed to the chair of physics at the University; he served as the professor of physics for the next 26 years. He also published numerous papers dealing with mechanics which mainly focused on the problems connected with vibrating strings. Daniel worked with Euler on elasticity as well as on the development of the Euler-Bernoulli beam equation. He also authored the ‘Specimen theoriae novae de mensura sortis (Exposition of a New Theory on the Measurement of Risk)’ which is the basis of an economic theory of risk aversion, risk premium, and utility.
In his 1738 book ‘Specimen theoriae novae de mensura sortis’ (Exposition of a New Theory on the Measurement of Risk), Bernoulli offered a solution to the St. Petersburg paradox as the basis of the economic theory of risk aversion, risk premium, and utility. Daniel Bernoulli often noticed that when making decisions that involved some uncertainty, people did not always try to maximize their possible monetary gain, but rather tried to maximize “utility”, an economic term encompassing their personal satisfaction and benefit. Bernoulli realized that for humans, there is a direct relationship between money gained and utility, but that it diminishes as the money gained increases. For example, to a person whose income is $10,000 per year, an additional $100 in income will provide more utility than it would to a person whose income is $50,000 per year. One of the earliest attempts to analyze a statistical problem involving censored data was Bernoulli’s 1766 analysis of smallpox morbidity and mortality data to demonstrate the efficacy of vaccination.
Daniel Bernoulli’s later works comprised of statistics and probability. His last work involved the application of probability theory to various practical matters, such as inoculation and relative proportion of male and female births.
Awards and Honor
Between 1725 and 1749 Daniel won 10 prizes from the Paris Academy of Sciences for work on astronomy, gravity, tides, magnetism, ocean currents, and the behavior of ships at sea. He also made substantial contributions in probability.
In 1732 Daniel accepted a post in botany and anatomy at Basel; in 1743, one in physiology; and in 1750, one in physics.
In May 1750, Daniel Bernoulli was elected a Fellow of the Royal Society.
Death and Legacy
On March 17, 1782, Daniel Bernoulli died at the age of 82, in Basel, Switzerland.
His most remarkable work was the ‘Bernoulli’s theorem’, related to the field of hydrodynamics. It states, in effect, that the total mechanical energy of the flowing fluid, comprising the energy associated with fluid pressure, the gravitational potential energy of elevation, and the kinetic energy of fluid motion, remains constant. The theorem still forms the basis of many engineering applications, such as aircraft wing design. Daniel also established the basis for the kinetic theory of gases and heat by demonstrating that the impact of molecules on a surface would explain pressure and that, assuming the constant, random motion of molecules, pressure and motion increase with temperature.
In 2002, Daniel Bernoulli was inducted into the International Air & Space Hall of Fame at the San Diego Air & Space Museum.
Information Source: