Biography of Kurt Gödel
Kurt Gödel – Austro-Hungarian-born Austrian, and later American, logician, mathematician, and philosopher.
Name: Kurt Friedrich Gödel
Date of Birth: April 28, 1906
Place of Birth: Brünn, Austria-Hungary
Date of Death: January 14, 1978 (aged 71)
Place of Death: Princeton, New Jersey, United States
Occupation: Mathematician, Philosopher
Father: Rudolf Gödel
Mother: Marianne Gödel
Spouse/Ex: Adele Nimbursky Porkert (m. 1938-1978)
Early Life

An Austrian-born mathematician, logician, and philosopher who obtained what may be the most important mathematical result of the 20th century, Kurt Gödel was born April 28, 1906, in Brünn, Austria-Hungary (now Brno, Czech Republic) into the German family of Rudolf Gödel (1874-1929), the manager of a textile factory, and Marianne Gödel (née Handschuh, 1879-1966). His famous incompleteness theorem, which states that within any axiomatic mathematical system there are propositions that cannot be proved or disproved on the basis of the axioms within that system; thus, such a system cannot be simultaneously complete and consistent. This proof established Gödel as one of the greatest logicians since Aristotle, and its repercussions continue to be felt and debated today.
Considered along with Aristotle, Alfred Tarski and Gottlob Frege to be one of the most significant logicians in history, Gödel had an immense effect upon scientific and philosophical thinking in the 20th century, a time when others such as Bertrand Russell, Alfred North Whitehead, and David Hilbert were analyzing the use of logic and set theory to understand the foundations of mathematics pioneered by Georg Cantor.
Gödel was a bright and inquisitive child, who had an interest in various subjects. Although he entered the University of Vienna with physics, he continued attending mathematics and philosophy classes and subsequently took up mathematics as his main subject. Soon after earning his doctorate degree at the age of twenty-five, he published two incompleteness theorems. Thereafter, he began working at the University of Vienna as Privatdozent. Concurrently, he also became a visiting professor at the Institute of Advanced Study at Princeton, USA. When Germany annexed Austria, he moved to the USA, where he spent his entire career at IAS, Princeton.
Gödel also showed that neither the axiom of choice nor the continuum hypothesis can be disproved from the accepted axioms of set theory, assuming these axioms are consistent. The former result opened the door for mathematicians to assume the axiom of choice in their proofs. He also made important contributions to proof theory by clarifying the connections between classical logic, intuitionistic logic, and modal logic.
Although Gödel was basically a mathematician, later his interest shifted towards philosophy and he continued working on these two subjects. Unfortunately, towards the end of life, he developed Persecutory delusions and fearing being poisoned, he starved himself to death.
Childhood, Family and Educational Life

Kurt Gödel, Gödel also spelled Goedel (/ˈɡɜːrdəl/; German: ˈkʊɐ̯t ˈɡøːdl̩), was born on April 28, 1906, in Brno, the second largest city in the Czech Republic. At the time of his birth, it was a textile-producing city in the Austro-Hungarian province of Moravia and was known as Brünn. His father, Rudolf Gödel, was initially a textile worker. Later, he became the manager and eventually the part owner of the Friedrich Redlich textile factory. His mother, Marianne Gödel (née Handschuh) was educated at a French institute; she had broad cultural interests.
At the time of his birth, the city had a German-speaking majority which included his parents. His father was Catholic and his mother was Protestant and the children were raised Protestant. The ancestors of Kurt Gödel were often active in Brünn’s cultural life. For example, his grandfather Joseph Gödel was a famous singer of that time and for some years a member of the Brünner Männergesangverein (Men’s Choral Union of Brünn).
There is a long list of citizenships that Gödel took up. At the age of 12, he received the Czechoslovak citizenship when the Austro-Hungarian Empire broke up. He always felt excommunicated in Czechoslovak so when he became an adult he chose Austrian citizenship. Subsequently, Germany annexed Austria and in consequence Austrian citizens became German, so did Gödel in 1938. Post World War II, he moved to America where he applied for American citizenship.
Gödel had a very happy childhood. He was very devoted to his mother and felt helpless when she was not around. He was also very inquisitive and kept on asking questions. Because of that, his family called him Herr Warum or Mr. Why. However, from his childhood, he suffered from different ailments. At the age of five, he had a mild anxiety neurosis but recovered completely from it. At six, he suffered from rheumatic fever. Although he recovered from this too, he became convinced that his heart had been damaged permanently.
Gödel attended the Evangelische Volksschule, a Lutheran school in Brünn from 1912 to 1916, and was enrolled in the Deutsches Staats-Realgymnasium from 1916 to 1924, excelling with honors in all his subjects, particularly in mathematics, languages, and religion. Although Kurt had first excelled in languages, he later became more interested in history and mathematics. His interest in mathematics increased when in 1920 his older brother Rudolf (born 1902) left for Vienna to go to medical school at the University of Vienna. During his teens, Kurt studied Gabelsberger shorthand, Goethe’s Theory of Colours and criticisms of Isaac Newton, and the writings of Immanuel Kant.
However, when Kurt Gödel joined the University of Vienna in 1924, he took up theoretical physics as his major. Sometime before this, he had read Goethe’s theory of colors and became interested in the subject. At the same time, he attended classes in mathematics and philosophy as well. Soon he came in contact with great mathematicians and in 1926, influenced by number theorist Philipp Furtwängler, he decided to change his subject and take up mathematics. Besides that, he was highly influenced by Karl Menger’s course in dimension theory and attended Heinrich Gomperz’s course in history of philosophy. Also in 1926, he entered the Vienna Circle, a group of positivist philosophers formed around Moritz Schlick, and until 1928, attended their meetings regularly. After graduation, he started working for his doctoral degree under Hans Hahn. His dissertation was on the problem of completeness.
In 1929, at the age of 23, Gödel completed his doctoral dissertation under Hans Hahn’s supervision. In it, he established his eponymous completeness theorem regarding the first-order predicate calculus. He was awarded his doctorate in 1930, and his thesis (accompanied by some additional work) was published by the Vienna Academy of Science.
Personal Life
In 1927, Kurt Gödel met Adele Nimbursky (née Porkert) at a night club, where she was employed as a dancer. She was six years older to him and a divorcee. Although his family did not approve of the match, he married her on September 20, 1938, just before they left for the U.S.A. Late in life he began to suffer from Persecutory delusions and feared of being poisoned. He did not take any food unless his wife prepared it.
Gödel was a convinced theist, in the Christian tradition. He held the notion that God was personal. He believed firmly in an afterlife, stating: “Of course this supposes that there are many relationships which today’s science and received wisdom haven’t any inkling of. But I am convinced of this the afterlife, independently of any theology.” It is “possible today to perceive, by pure reasoning” that it “is entirely consistent with known facts.” “If the world is rationally constructed and has meaning, then there must be such a thing as an afterlife.”
Career and Works

Kurt Gödel joined the faculty at the University of Vienna in 1930. During that period, Vienna was one of the intellectual hubs of the world. It was home to the famed Vienna Circle, a group of scientists, mathematicians, and philosophers who endorsed the naturalistic, strongly empiricist, and antimetaphysical view known as logical positivism. Gödel’s dissertation adviser, Hans Hahn, was one of the leaders of the Vienna Circle, and he introduced his star student to the group. However, Gödel’s own philosophical views could not have been more different from those of the positivists. He subscribed to Platonism, theism, and mind-body dualism. In addition, he was also somewhat mentally unstable and subject to paranoia—a problem that grew worse as he aged. Thus, his contact with the members of the Vienna Circle left him with the feeling that the 20th century was hostile to his ideas.
In 1930 Kurt Gödel attended the Second Conference on the Epistemology of the Exact Sciences, held in Königsberg, 5-7 September. Here he delivered his incompleteness theorems. Kurt Gödel published his incompleteness theorems in Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (called in English “On Formally Undecidable Propositions of Principia Mathematica and Related Systems”). In that article, he proved for any computable axiomatic system that is powerful enough to describe the arithmetic of the natural numbers (e.g., the Peano axioms or Zermelo–Fraenkel set theory with the axiom of choice), that:
- If a (logical or axiomatic formal) system is consistent, it cannot be complete.
- The consistency of axioms cannot be proved within their own system.
These theorems ended a half-century of attempts, beginning with the work of Frege and culminating in Principia Mathematica and Hilbert’s formalism, to find a set of axioms sufficient for all mathematics.
Also in 1933, Gödel was appointed a visiting professor at the Institute for Advanced Study, Princeton, U.S.A. Accordingly, from February to May 1934, he gave a series of lectures titled ‘On undecidable propositions of formal mathematical systems’ at the IAS. These lectures were noted down by young Stephen Cole Kleene, an American mathematician and later published in book form. Some time now, Gödel also met Albert Einstein and established a life-long friendship. In the mid-1930s, his mental health deteriorated and he suffered a nervous breakdown. Thereafter, he spent several months in a sanatorium receiving treatment for depression. His bout of depression reappeared when in June 1936, German philosopher Moritz Schlick was murdered by a deranged student. Gödel again had to undergo treatment. Thus he could not return to his academic life until 1937.
Subsequently, Gödel left for another visit to the United States, spending the autumn of 1938 at the IAS and publishing Consistency of the axiom of choice and of the generalized continuum-hypothesis with the axioms of set theory, a classic of modern mathematics. In that work, he introduced the constructible universe, a model of set theory in which the only sets that exist are those that can be constructed from simpler sets. Gödel showed that both the axiom of choice (AC) and the generalized continuum hypothesis (GCH) are true in the constructible universe, and therefore must be consistent with the Zermelo–Fraenkel axioms for set theory (ZF). This result has had considerable consequences for working mathematicians, as it means they can assume the axiom of choice when proving the Hahn-Banach theorem. Paul Cohen later constructed a model of ZF in which AC and GCH are false; together these proofs mean that AC and GCH are independent of the ZF axioms for set theory. Gödel spent the spring of 1939 at the University of Notre Dame.
Furthermore, during his stay in America Gödel developed the ideas of computability and recursive functions. He even delivered a lecture on the subject. In Princeton, the Institute for Advanced Study invited him to conduct a series of lectures in 1934 and they were later published. Kurt Gödel married a divorced dancer, an older woman, Adele Nimbursky, after much opposition by his parents.
On March 12, 1938, Germany annexed Austria. They abolished the position of Privatdozent and so Gödel had to apply afresh. All along, he had been close to several Jewish scholars and this went against him. He was not only turned down for an academic post but also found physically fit for conscription into the Nazi army.
World War II started in September 1939. Before the year was up, Gödel and his wife left Vienna for Princeton. To avoid the difficulty of an Atlantic crossing, the Gödels took the Trans-Siberian Railway to the Pacific, sailed from Japan to San Francisco (which they reached on March 4, 1940), then crossed the US by train to Princeton. There Gödel accepted a position at the Institute for Advanced Study (IAS), which he had previously visited during 1933-34. Gödel and his wife, Adele, spent the summer of 1942 in Blue Hill, Maine, at the Blue Hill Inn at the top of the bay. Gödel was not merely vacationing but had a very productive summer of work. Using Heft 15 of Gödel’s still-unpublished Arbeitshefte (working notebooks), John W. Dawson Jr. conjectures that Gödel discovered a proof for the independence of the axiom of choice from finite type theory, a weakened form of set theory, while in Blue Hill in 1942. Gödel’s close friend Hao Wang supports this conjecture, noting that Gödel’s Blue Hill notebooks contain his most extensive treatment of the problem.
From 1943 to 1946, Gödel concentrated mainly on Gottfried Leibniz but also studied Immanuel Kant and Edmund Husserl. Meanwhile, in 1944, he published his first philosophical paper, titled ‘On Russell’s Mathematical Logic.’ During this period, Gödel also had a quiet social life and spent a lot of time with Albert Einstein discussing everything from politics to philosophy and physics. Later he also became friendly with Morgenstern.
In 1946, Gödel was made a permanent member of the IAS. In 1947, he published his second paper on philosophy, titled ‘What is Cantor’s Continuum Hypothesis?’ Sometimes now, he also studied the U.S. Constitution and discovered an inconsistency, which could allow the United States to become a dictatorship. Therefore, when on December 5, 1947, he was asked to appear for his U.S. citizenship examination, Einstein and Morgenstern accompanied him. They were afraid, that Gödel might say something that would jeopardize his chances. However, everything went on smoothly and Gödel became a US citizen. He then continued working on philosophy and in 1949 published his paper on the subject, ‘A Remark on the Relationship between Relativity Theory and Idealistic Philosophy.’
In 1949, Gödel demonstrated the existence of solutions involving closed timelike curves, to Einstein’s field equations in general relativity. He is said to have given this elaboration to Einstein as a present for his 70th birthday. His “rotating universes” would allow time travel to the past and caused Einstein to have doubts about his own theory. His solutions are known as the Gödel metric (an exact solution of the Einstein field equation).
In 1953, Gödel became a full professor at the Institute. By that time, his involvement in philosophy had deepened. From then on until 1959, he worked on a submission to the Schilpp volume on Rudolf Carnap. Titled ‘Is Mathematics a Syntax of Language?’ It for some reason was never published.

In 1964 Gödel published a philosophical paper, “What Is Cantor’s Continuum Problem?,” in which he proposed a solution to an ancient objection to Platonism. It is often argued that Platonism cannot be true, because it makes mathematical knowledge impossible: whereas humans seem to acquire all knowledge of the external world through sensory perception, Platonism asserts that mathematical objects, such as numbers, are nonphysical objects that cannot be perceived by the senses. Gödel responded to this argument by claiming that, in addition to the normal five senses, humans also possess a faculty of mathematical intuition, a faculty that enables people to grasp the nature of numbers or to see them in the mind’s eye. Gödel’s claim was that the faculty of mathematical intuition makes it possible to acquire knowledge of nonphysical mathematical objects that exist outside of space and time.
Gödel remained with the Institute until his retirement in 1976. Thereafter he remained attached to it as an emeritus professor. In his later years, although he worked consistently, he did not publish any paper. However, he circulated many of them in manuscript form. ‘Some considerations leading to the probable conclusion that the true power of the continuum is ℵ2’ and ‘Ontologischer Beweis’, both circulated in 1970, are some such works. Together they give expression to his core ideas, resulting from his long involvement with mathematics and philosophy.
Awards and Honor
Kurt Gödel was awarded (with Julian Schwinger) the first Albert Einstein Award in 1951 and was also awarded the National Medal of Science, in 1974.
In 1968, Gödel was elected a Foreign Member of the Royal Society.
Gödel was a Plenary Speaker of the ICM in 1950 in Cambridge, Massachusetts. The Gödel Prize, an annual prize for outstanding papers in the area of theoretical computer science, is named after him.
Death and Legacy
As Gödel aged, he grew more and more paranoid and eventually became convinced that he was being poisoned. He refused to eat unless his wife tasted his food first. When she became ill and had to be hospitalized for an extended period of time, Gödel essentially stopped eating and starved to death.
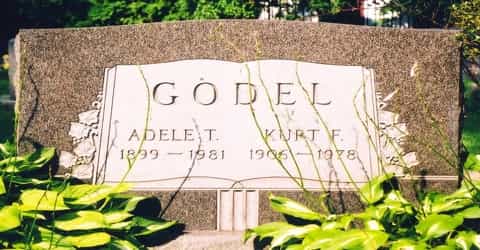
Kurt Gödel was admitted to Princeton Hospital, where he died on January 14, 1978. His death certificate stated that he died of “malnutrition and inanition caused by personality disturbance”. He was buried in Princeton Cemetery. Adele’s death followed in 1981.
Gödel is best remembered for his two incompleteness theorems, published in 1931. While working on mathematical logic, he discovered that there were some inherent limitations in every formal axiomatic system containing basic arithmetic. Later these theorems were found to be as much important for mathematical logic as for the philosophy of mathematics.
Concepts like Gödel metric, Gödel numbering, and Gödel’s ontological proof bear his legacy. The Kurt Gödel Society, an international organization founded in 1987 for the promotion of research in logic, philosophy, and the history of mathematics, was named in his honor.
Information Source: