Break-Even Analysis
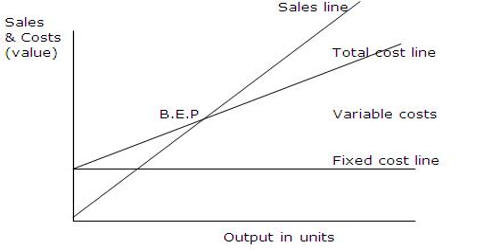
Break-Even Analysis in economics, business, and cost accounting refers to the point in which total cost and total revenue are equal. It is that part of Cost-Volume-Profit Analysis which tells us about the level of sales at which revenues equals expenses thus showing a zero net income more precisely, such a sales point is called Break-Even Point. It is used to locate the sales volume at which a business earns exactly no money, where all contribution margin earned is needed to pay for the company’s fixed costs. CVP analysis is sometimes referred to simply as a break-even analysis. This is unfortunate because break-even analysis is just one part of the entire CVP analysis.
The contribution margin is the margin that results when all variable expenses are subtracted from revenue. When the breakeven point is near the maximum sales level of a business, this means it is nearly impossible for the company to earn a profit even under the best of circumstances. Yet, it is always taken as an important part of profit planning as it gives the planner many insights into the data with which he or she is working. The profit planning of each firm begins with a break-even analysis. In addition, breakeven analysis is useful for establishing the overall ability of a company to generate a profit.
The formula for Break-Even Analysis:
Break-even quantity = Fixed costs / (Sales price per unit – Variable cost per unit)
Where:
- Fixed costs are costs that do not change with varying output (e.g., salary, rent, building machinery).
- The sales price per unit is the selling price (unit selling price) per unit.
- Variable cost per unit is the variable costs incurred to create a unit.
Example: Suppose, annual fixed costs of the Rexona company are $ 100,000, selling price is $ 25 per unit, variable costs per unit is $ 15, contribution margin per unit(CMPU) is $ 10 and contribution margin ratio(C/M) is 40%. Calculate the Rexona,s break-even point(BEP) in units and in $.
Solution,
Rexona’s Break-even Point(BEP)
- BEP(in units) = Fixed Costs/CMPU = $ 100,000/$ 10 = 10,000 units
- BEP(in $) = Fixed Costs/C/M ratio = $100,000/0.40 = $ 250,000.
Breakeven analysis is useful for the following reasons:
- Determining the amount of remaining capacity after the breakeven point is reached, which reveals the maximum amount of profit that can be generated.
- Determining the impact on profit if automation (a fixed cost) replaces labor (a variable cost).
- Determining the change in profits if product prices are altered.
- Determining the number of losses that could be sustained if the business suffers a sales downturn.