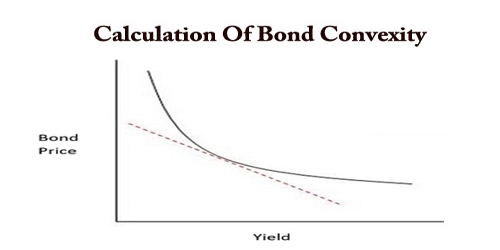
Convexity could be a measure of the curve within the relationship between a bond’s price and a bond’s yield. In finance, bond convexity could be a measure of the non-linear relationship of bond prices to changes in interest rates, the second derivative of the worth of the bond with regard to interest rates (duration is that the first derivative).
In general, the upper the duration, the more sensitive the bond price is to the change in interest rates. Bond convexity is one in all the foremost basic and widely used varieties of convexity in finance. Convexity has supported the work of Hon-Fei Lai and popularized by Stanley Diller.
For example, the rule of thumb considered the relationship between yield and price to be linear (a straight line). For every X% change in interest rates, bond prices increased or decreased by the duration multiplied by X%. Convexity says that relationship is not linear. In fact, it’s curved, with a steeper slope as interest rates decrease and a lower slope as interest rates increase.
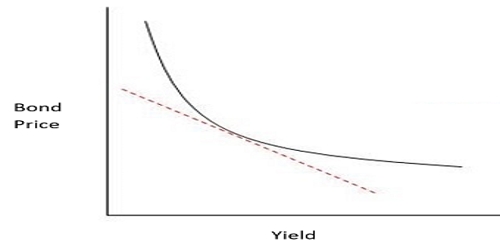
The x-axis is interest rates (yield), and the y-axis is the bond’s price. The curved line is the actual bond price at different levels of interest rates. The straight dotted line is the bond price if there was no convexity. In other words, it’s the bond price using our simple rule of thumb mentioned in the introduction. Convexity, then, is the difference between the two lines. It measures and accounts for the curvature in actual bond prices.
Calculation of convexity –
Bond Convexity Formula:
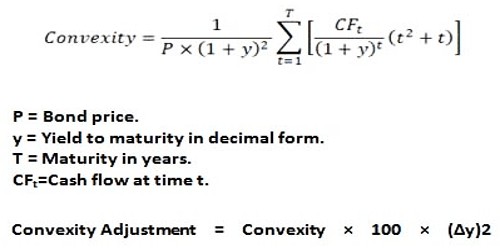
Duration is a linear measure or 1st derivative of how the price of a bond changes in response to interest rate changes. As interest rates change, the price is not likely to change linearly, but instead, it would change over some curved function of interest rates. The more curved the price function of the bond is, the more inaccurate duration is as a measure of the interest rate sensitivity.
Convexity is a measure of the curvature or 2nd derivative of how the price of a bond varies with an interest rate, i.e. how the duration of a bond changes as the interest rate changes. Specifically, one assumes that the interest rate is constant across the life of the bond, and that changes in interest rates occur evenly. Using these assumptions, the duration can be formulated as the first derivative of the price function of the bond with respect to the interest rate in question. Then the convexity would be the second derivative of the price function with respect to the interest rate.
For a Bond of Face Value USD1,000 with a semi-annual coupon of 8.0% and a yield of 10% and 6 years to maturity and a present price of 911.37, the duration is 4.82 years, the modified duration is 4.59 and the calculation for Convexity would be:
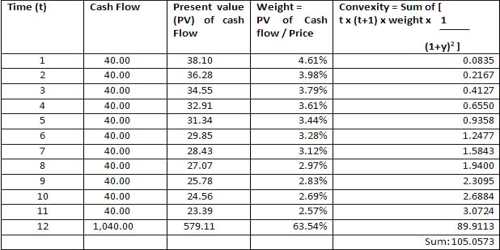
Annual Convexity: Semi-Annual Convexity/ 4= 26.2643Semi Annual Convexity: 105.0573
In the above example, a convexity of 26.2643 can be used to predict the price change for a 1% change in yield would be:
If the only modified duration is used:
Change in price = – Modified Duration × Change in yield
Change in price for 1% increase in yield = (– 4.59×1%) = -4.59%
So the price would decrease by 41.83
In actual markets, the assumption of constant interest rates and even changes is not correct, and more complex models are needed to actually price bonds. However, these simplifying assumptions allow one to quickly and easily calculate factors that describe the sensitivity of the bond prices to interest rate changes.
Convexity does not assume the relationship between Bond value and interest rates to be linear. For large fluctuations in interest rates, it is a better measure than duration.
Information Sources: