The capital market line (CML) is a theoretical principle that determines the best risk-free asset and market portfolio combinations. It’s a tangent line drawn from the risk-free asset’s point to the risky asset’s feasible field. The CML addresses portfolios that ideally join hazard and return; the Capital asset pricing model (CAPM), portrays the compromise among hazard and return for proficient portfolios. The CML is better than Efficient Frontier as in it joins unsafe resources with hazard-free resources. According to CAPM, all investors can prefer an equilibrium position on the capital market line by borrowing or lending at the risk-free rate, which maximizes return for a given level of risk.
The CML is an uncommon adaptation of the Capital Allocation Line (CAL). The CAL shows a proficient boondocks for an arrangement of hazardous resources. The intersection point M addresses the market portfolio, so named since every single levelheaded financial backer (least fluctuation basis) should hold their dangerous resources in similar extents as their loads in the market portfolio. The most effective portfolio is the tangency portfolio, which is determined by the intersection point of CML and the efficient frontier. If the sharpe ratio is above CML, buy assets; if the sharpe ratio is below CML, sell.
Moving the CML up will increase the portfolio’s risk, while moving it down will reduce it. As a result, the return expectation will rise or fall, depending on the situation. A weighted percentage of risk-free assets is included in the CML. The risk-return assumption becomes linear as a result, while the CAL is a curved frontier. The equation for the CML is:
E(Rc) = y × E(RM) + (1 – y) × RF
Where:
y is a proportion of a market portfolio,
E(RM) is an expected return of a market portfolio,
(1-y) is a proportion of a risk-free asset, and
RF is a risk-free rate.
Given a particular mix of assets and the risk associated with them, all investors would select the same market portfolio.
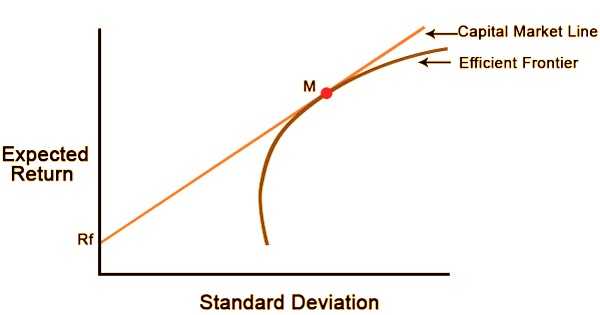
The CML varies from the more famous effective outskirts in that it incorporates hazard free ventures. The capture point of CML and productive boondocks would bring about the most effective portfolio, called the intersection portfolio. With the exception of the Market Portfolio, which is the tangent to the efficient frontier, all points along the CML have superior risk-return profiles to any portfolio on the efficient frontier. From a CML viewpoint, the portfolio M is made altogether out of the dangerous resource, the market, and has no holding of the danger free resource, i.e., cash is neither put resources into, nor acquired from the currency market account. Focuses to one side of or more the CML are infeasible, while focuses to one side/beneath are feasible yet wasteful.
The CML (Capital Market Line) depicts a particular portfolio’s rates of return, while the SML (Security Market Line) depicts market risk as well as a specific time return. It also displays the estimated returns on individual properties. The CML stands for absolute risk, and the SML measures it (beta or systematic risk). Fairly priced securities always plot on the SML and CML. Note that protections which create higher outcomes for a specific danger, are for the most part over the SML or CML, and are consistently undervalue and the other way around. Capital Market Theory attempts to clarify the development of the Capital Markets after some time utilizing one of the numerous numerical models. The most usually utilized model in the Capital Market Theory is the Capital Asset Pricing Model.
Buying assets with a Sharpe ratio above the CML and selling assets with a Sharpe ratio below the CML is a stock picking rule of thumb. Indeed, the efficient market theory states that beating the market is unlikely. Depending on their risk aversion, individual investors will keep either the risk-free asset or a combination of the risk-free asset and the market portfolio. As a financial backer climbs the CML, the general portfolio hazard and bring increments back. In this way, all portfolios ought to have a Sharpe proportion not exactly or equivalent to the market’s.
Investors that are risk averse would choose portfolios that are similar to the risk-free asset, choosing low volatility over higher returns. Investors that are less risk averse would favor portfolios that are higher on the CML, with a higher expected return but more volatility. In result, if there is a portfolio (or resource) whose Sharpe proportion will be greater than the market’s then this portfolio (or resource) has a better yield for each unit of hazard, which repudiates the productive market speculation. There are sure suppositions that exist inside the idea of Capital Market Line. In the real world, however, these assumptions are often broken. Markets, for example, are not frictionless. The transactions have certain costs associated with them.
Furthermore, investors are rarely fair. They always make decisions based on feelings and sentiments. By getting assets at the danger free rate, they can likewise contribute over 100% of their investable assets in the hazardous market portfolio, expanding both the normal return and the danger past that offered by the market portfolio. Theoretically, investors can borrow and lend at the risk-free rate without any restrictions.
In the real world, however, borrowers typically borrow at a higher rate than they are willing to lend. A leveraged portfolio’s probability or standard deviation rises as a result of this. Theoretically, portfolios that fall on the capital market line (CML) maximize the risk/return relationship, resulting in maximum efficiency. Along these lines, the incline of the CML is the Sharpe proportion of the market portfolio. The suspicion for the CML depends on the suppositions of the capital market hypothesis. However, these suppositions regularly don’t remain constant in reality. Analysts also use the Capital Market Line to calculate the amount of return that investors can expect if they take a certain amount of risk in their portfolio.
Information Sources: