The sensitivity of a bond or bond portfolio to a 100-basis point 1% change in yield at a given maturity point is measured by key rate duration. A single risk metric for interest-rate sensitivity is insufficient for managers who need to account for changes in the shape of the yield curve in detail, and a more thorough means of evaluating changes throughout the whole term structure is necessary. It is viewed as an improvement over-utilizing the powerful span metric, which must be applied when there are equal chances in the yield the whole way across the yield curve.
The key rate duration is used to assess how sensitive a debt security’s price is to a one percent change in yield for a certain maturity while all other maturities are maintained constant with regard to other maturities. Utilizing the measurement can help financial backers or monetary investigators foresee the plausible productivity of putting resources into bonds with different developments. When keeping different developments steady, the key rate length is utilized to gauge the affectability in an obligation security’s cost to a 1% change in yield for a particular development.
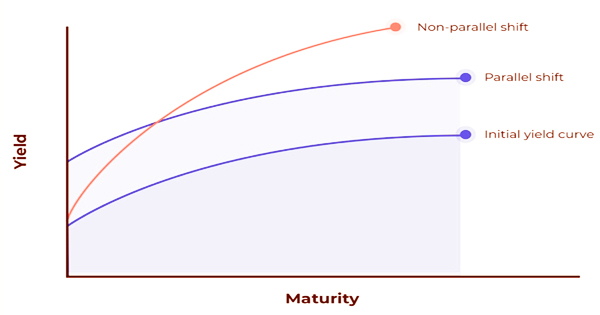
The use of key-rate durations (KRDs), proposed by Thomas Ho, is one of the most prevalent methods for accomplishing this (1992). On the yield curve, Ho identifies a number of maturities as important rate lengths, with typical values of 3 months, 1, 2, 3, 5, 7, 10, 15, 20, 25, and 30 years. The key rate duration is seen to be a better measure than the effective duration. It is on the grounds that the viable length metric is simply pertinent to resemble shifts in financing costs and the yield bend when loan fees for all the different security developments at the same time increment or diminishing by a similar sum.
Here, we will look at the key rate duration formula and understand it better with an example,
Key rate duration = P− − P+ / 2∗0.01∗P0
Where –
P– − Price of bond after 1% decreases in profit.
P+ − Price of bond after 1% increase in profit.
P0 − Original price of the bond
Assume a bond is initially valued at $1,000, and with a 1% rise in yield, it would be priced at $970, and with a 1% drop in yield, it would be priced at $1,040. The key rate duration for this bond would be based on the calculation above:
KRD = ($1,040−$970) / (2×1%×$1,000) = $70 / $20 = 3.5
where:
KRD = Key rate duration
All things considered, such a marvel infrequently, if at any time, happen. Loan cost increments or diminishes for momentary securities don’t ordinarily resemble rate increments or diminishes for the long haul or medium-term securities. In reality, interest rates for various bond maturities may be going in opposing directions, with long-term interest rates rising while short-term interest rates fall.
In other words, the effect of a change in the yield curve that is concentrated at a certain maturity and limited to the immediate neighborhood of that maturity, generally by having the change decrease linearly to zero at surrounding points, is measured by a key rate duration. The anticipated change in esteem coming about because of an adjustment of the yield on a security or security portfolio with a given development is addressed by the key rate length. It is hypothetically expected that the yields for any remaining developments would stay steady.
Effective time frame Another significant bond metric is an informative duration measure, which predicts projected price changes for a bond or portfolio of bonds given a 1% change in yield, although it is only applicable for yield curve parallel movements. The key rate term addresses an improvement over the powerful length measure since it shows anticipated changes in value/esteem when there are shifts in the yield bend that are not equal across all developments.
The modified duration of an instrument is approximately equal to the sum of its key rate durations. Because adjusted duration implies a flat yield curve, which is rarely the case, the total may not be precise. Expecting that a financial backer’s loan fee forecasts end up being right throughout a given time-frame, they can utilize the key rate term metric to figure out which security developments are probably going to give the most productive venture returns.
Therefore, the measurement might be utilized to analyze diverse potential fixed-pay ventures. Key rate duration and successful term are connected. There are 11 developments along the Treasury spot rate bend, and a key rate length might be determined for each. It represents the projected change in value for a bond or bond portfolio with a given maturity as a result of a yield shift. It is assumed that all other maturities’ yields remain constant.
It’s tough to understand an individual key rate duration because it’s extremely rare that a single point on the Treasury yield curve would go upwards or lower while the rest of the curve remains unchanged. Accordingly, the measurement can be utilized to think about different imminent fixed-pay ventures. It’s helpful for seeing key rate lengths across the bend and taking a gander at the general upsides of key rate spans between two protections.
Information Sources: