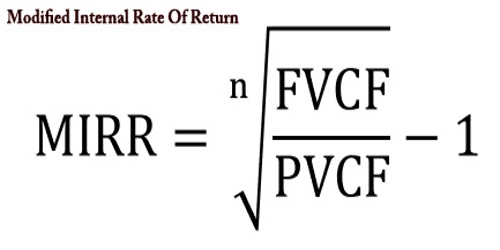The modified internal rate of return (commonly denoted as MIRR) assumes that positive cash flows are reinvested at the firm’s cost of capital and that the initial outlays are financed at the firm’s financing cost. By contrast, the traditional internal rate of return (IRR) assumes the cash flows from a project are reinvested at the IRR itself. The MIRR, therefore, more accurately reflects the cost and profitability of a project.
While there are several problems with the IRR, MIRR resolves two of them.
Firstly, IRR is sometimes misapplied, under the assumption that interim positive cash flows are reinvested at the same rate of return as that of the project that generated them. This is usually an unrealistic scenario and a more likely situation is that the funds will be reinvested at a rate closer to the firm’s cost of capital. The IRR therefore often gives an unduly optimistic picture of the projects under study. Generally, for comparing projects more fairly, the weighted average cost of capital should be used for reinvesting the interim cash flows.
Secondly, more than one IRR can be found for projects with alternating positive and negative cash flows, which leads to confusion and ambiguity. MIRR finds only one value.
MIRR’s Formula and Calculation –
Given the variables, the formula for MIRR is expressed as:

Where:
FVCF(c) = the future value of positive cash flows at the cost of capital for the company
PVCF(fc) = the present value of negative cash flows at the financing cost of the company
n = number of periods
Meanwhile, the internal rate of return (IRR) is a discount rate that makes the net present value (NPV) of all cash flows from a particular project equal to zero. Both MIRR and IRR calculations rely on the formula for NPV.
Generally, the manual calculation of the MIRR is a tedious process that is prone to making mistakes. Alternatively, the MIRR can be easily calculated in spreadsheet applications such as Microsoft Excel. For example, in MS Excel, it can be calculated using the function called “=MIRR (cash flows, financing rate, reinvestment rate).”
The MIRR is primarily used in capital budgeting to identify the viability of an investment project. For instance, if the MIRR of a project is higher than its expected return, an investment is considered to be attractive.
Conversely, it is not recommended to undertake a project if it’s MIRR is less than the expected return. In addition, the MIRR is commonly employed to compare several alternative projects that are mutually exclusive. In such a case, the project with the highest MIRR is the most attractive.
The MIRR allows project managers to change the assumed rate of reinvested growth from stage to stage in a project. The most common method is to input the average estimated cost of capital, but there is the flexibility to add any specific anticipated reinvestment rate.
Example of MIRR –
Let’s consider the following example. Company A wants to assess the investment viability of its upcoming project of building a new plant. The company must spend $200 million on the plant’s construction. At the same time, it expects that the new plant will generate revenues of $50 million in the first year, $100 million in the second year, and $150 million in the third year. Note that the cost of capital of Company A is 10%.
Using the information above, we may calculate the modified internal rate of return of the project. First, we need to calculate the future value of positive cash flows at the reinvestment rate. We may assume that the reinvestment rate equals the company’s cost of capital.
The present value of negative cash flows discounted at the financing rate is simply $200 million because there is only one cash outflow occurring before the project. Therefore, we can use the variables to calculate the modified internal rate of return (MIRR):
The modified internal rate of return for the project is 17.02%. In order to determine the investment viability of the project, the figure may be later compared with the expected return of the project.
Like the internal rate of return (IRR), the modified internal rate of return is not valid for ranking projects of different sizes, because a larger project with a smaller modified internal rate of return may have a higher net present value. However, there exist variants of the modified internal rate of return which can be used for such comparisons.
Information Sources: