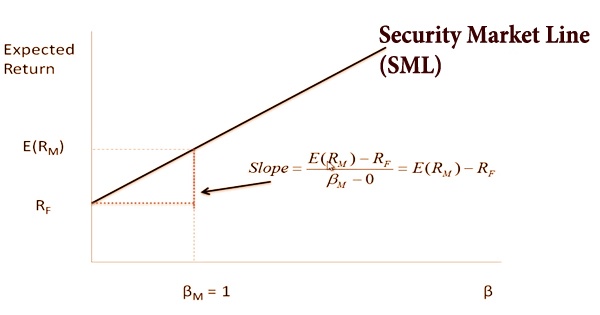
The security market line (SML) is a representation of the capital asset pricing model (CAPM) that plots different levels of systemic, or market risk, of various marketable securities against the market’s expected to return at any given time. It calculates the market’s expected to return at various levels of systematic or market risk. It is additionally called ‘characteristic line’ where the x-axis addresses beta or the danger of the resources, and the y-axis addresses the normal return. SML is a hypothetical portrayal of the normal returns of resources dependent on precise, non-diversifiable danger.
A security’s market risk premium is calculated by where it is plotted on the map in relation to the SML. The probability of an individual risky security is determined by the uncertainty of the security’s return rather than the market portfolio’s return. The systemic risk is reflected in the risk of these individual risky securities. Idiosyncratic risk is excluded from the security market line. All the more extensively, the SML plots the normal market returns for an attractive security at a given degree of market hazard for the attractive security. The degree of hazard is dictated by the beta of protection from the market.
Security Market Line Equation:
The risk-free interest rate is the Y-intercept of the SML. The risk return tradeoff is reflected by the slope of the SML, which is equal to the market risk premium at any given time:
SML: E(Ri) = Rf + βi (E(RM) – Rf)
In the above security market line formula:
E(Ri) is the expected return on the security
Rf is the risk-free rate and represents the y-intercept of the SML
βi is a non-diversifiable or systematic risk. It is the most crucial factor in SML. We will discuss this in detail in this article.
E(RM) is expected to return on market portfolio M.
E(RM) – Rf is known as Market Risk Premium
The SML reflects the investment’s opportunity cost as used in portfolio management (investing in a combination of the market portfolio and the risk-free asset). The security market line is a venture assessment apparatus got from the CAPM a model that depicts hazard return relationship for protections and depends with the understanding that financial backers should be made up for both the time value of money (TVM) and the comparing level of hazard related with any speculation, alluded to as the danger premium. All the correctly priced securities are plotted on the SML.
The above equation can be graphically represented as below:
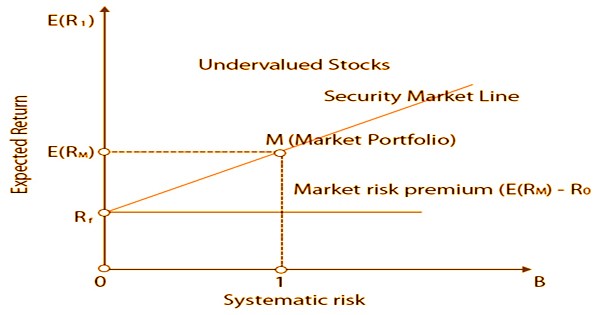
The security market line, on the other hand, is not always valid in practice because it is based on very broad assumptions that do not always hold true. The assets above the line are undervalued since they yield a higher return for a given amount of risk (beta). The resources underneath the line are exaggerated on the grounds that for a given measure of hazard, they yield a lower return. In a market in amazing balance, all protections would fall on the SML. The idea of beta is vital to the CAPM and the SML.
The beta of a security is a proportion of its methodical danger, which can’t be wiped out by expansion. The overall market average is described as a beta value of one. A beta value greater than one indicates a higher risk level than the market average, whereas a beta value less than one indicates a lower risk level than the market average.
Characteristics of the Security Market Line (SML) are as below:
- SML is an excellent reflection of investment opportunity expense, since it combines a risk-free asset and a stock portfolio.
- The expected return on a zero-beta security or zero-beta portfolio is equal to the risk-free rate.
- The slope of the Security Market Line is determined by market risk premium, which is: (E(RM) – Rf). Higher the market risk premium steeper the slope and vice-versa
- All the assets which are correctly priced are represented on SML.
- The assets above the SML are undervalued because they have a higher potential return for the same level of risk.
- Assets below the SML are overvalued because they provide lower expected returns for the same level of risk.
The security market line is ordinarily utilized by cash supervisors and financial backers to assess a speculation item that they’re considering remembering for a portfolio. The SML is helpful in deciding if the security offers an ideal expected return contrasted with its degree of hazard. The assumptions for CAPM also apply to SML since the security market line is a graphical representation of the capital asset pricing model (CAPM). CAPM is typically a one-factor model that is solely dependent on the degree of systemic danger that a security face.
A stock-picking dependable guideline for resources with positive beta is to purchase if the Treynor proportion will be over the SML and sell in the event that it will be beneath. To be sure, from the productive market theory, it follows that we can’t beat the market. If a security appears above the SML on the SML table, it is considered undervalued since the chart location means that the security provides a higher return against its inherent risk. The bigger the degree of methodical danger, the bigger the normal return for the security is more danger rises to more reward. It is a direct relationship and clarifies why the security market line is a straight line.
Slope of Securities Market Line (Beta): In the Security Market Line equation, beta (slope) is a critical variable. Beta is a measure of a security’s or a portfolio’s uncertainty or systemic risk when compared to the market as a whole. The market can be thought of as a universal asset basket or an indicative market index. If Beta = 1, then the stock has the same level of risk as to the market. A beta greater than one indicates a riskier asset than the market, while a beta less than one indicates a riskier asset than the market. While beta offers a single metric for assessing an asset’s volatility in relation to the market, beta does not remain constant over time.
The security market line can likewise be utilized to decide if a resource is overrated or undervalued, given its degree of methodical danger, contrasted with the market. In this way, all resources ought to have a Treynor proportion not exactly or equivalent to that of the market. As a result, if an asset’s Treynor ratio is higher than the market’s, that asset can provide a higher return for a given level of systematic risk (i.e., beta), contradicting the efficient market hypothesis. If the asset provides a higher return than the market for a given amount of systematic risk, it will be plotted above the security market line graphically.
If the asset provides a lower return for a given amount of systematic risk than the market, it will be plotted below the security market line. The SML is as often as possible utilized in looking at two comparative protections that offer around a similar return, to figure out which of them includes minimal measure of inalienable market hazard comparative with the normal return. The SML may also be used to compare securities with similar risk levels to see which one provides the best expected return for that level of risk.
Information Sources: