This report describes the products feature of ACI Motors and hire purchase system of Tractor business in ACI Motors of Bangladesh. This report is based on my working experience in ACI Motors. Three months effort on this organization was a worthwhile understanding for me as ACI is one of the leading reputed business organizations in Bangladesh. The study has assisted to know about the performance of the product of ACI Motors. At the same time to know about the credit policy that is very important for increasing sales. We also got to know conditions and
terms of hire purchase for purchasing Tractor.
The report has been divided mainly into two divisions then in some chapters, in order to put specific emphasis on different aspects. The first part is performance measurement and then credit system of Tractor Business of ACI Motors. In the performance measurement, I have interpreted the sales volume and sales value among the ACI Motors products like which product sales more and which one is more profitable for the company. We get the present scenario of each market by seeing the market position and share of these products from where. The report mentions about the facilities and benefits ACI Motors Limited provides to their customer. ACI have to come out with new ideas to grape customer of other brand user. They have to do give more additional value to the product, need to develop pricing strategy, improve communication with the customer for increasing sells.
Over I have discussed the credit system of Tractor in ACI. It should be more available and increase the time for installment to the customer that will attract them more compare to others. Credit sale sometimes makes discrimination in the country business. So, it needs proper planning, strategy and full organizing capability. Collection of credit is described in details in this chapter. I have discussed activities of the collection team.
However, there are certain information has been deliberately skipped in this report, as they had been qualified by the ACI as confidential information. The report also consist recommendations and conclusion according to my point of view, which I think would improve the environment of the organization if implemented.
Introduction:
Bangladesh economy depends heavily on agriculture. During financial year 2011-2012 agriculture sector alone had a contribution of 19.29% in the GDP growth. Though service sector brings almost half of economic earnings, two third of Bangladeshi people are engaged in agricultural activities. Major macroeconomic factors like employment generation, poverty improvement, human resources development and food security depends largely on the performance of the agriculture sector since it comprises about 30% of the country’s GDP and employing around 60% of the total labour force. Constant researches are being done in order to obtain advanced technologies so that new crops can be created and irrigation, harvesting and such steps of cultivation can be done more efficiently so that we, as a country, can attain food security. Agro based sector is continuing to grow with the use of advanced technology and modern machineries. In Bangladesh agricultural sector refers to crop cultivation (mainly rice, jute, wheat, sugar, cotton, vegetable, tea, tobacco etc.), animal farming (poultry, dairy etc.), forestry, fisheries and other related services etc. Competing with other nations, agribusiness of our country is moving fast towards excellence. To assure continuous progress in this industry we need to provide farmers modern machineries for cultivation. Keeping this in mind ACI Motors began its operation with a product range of agricultural machineries like tractor, power tiller, and diesel engine, combined harvester, Rice Transplanter, Pump and guaranteed supply of quality machineries and better after sales service.
All of these brands have got tremendous responses from farmers. ACI Motors is importing these quality products from China, India and other countries. ACI Motors operates sales activities by establishing sales and service centre in many parts of the country and appointing dealers all over Bangladesh. Since the real life business situation is always very complex and competitive, every business has to face the intense competition and successfully operate within this critical situation.
To stay and increase the pace in the business track, the perception and brand awareness is very important. Some of products like Tractor, Power Tiller, Rotavator are more expensive so customer not able to buy in cash. In these case ACI Motors allows them to buy them in credit where they can pay the payment over the period in installment.
Objective of the Study:
i. General Objective:
The primary objective of this report is to gather practical knowledge and experience for representing the actual situation of the agricultural machineries business in Bangladesh.
ii. Specific objective
I mainly discussed the ACI Motors approached to the agricultural machineries business. The performance of ACI motors products and the credit system. Some other secondary objective is also comparing the agricultural machineries business of our country, know about the Advance Chemical Industries (ACI) and present an overview and brief introduction of ACI Motors Ltd.
Methodology of the study:
Study Type: Descriptive Study
Analysis: Qualitative analysis based on observation.
Source of Data Collection:
To make the report more meaningful and presentable, I have use web site and documents. Information for this paper is mainly collected from various primary and secondary data sources.
i. Primary Sources:
Take Interviews and discussion with the Executive Logistic Support and other personnel of ACI Motors.
ii. Secondary Sources:
Information related to the company, is collected from internal and external sources the annual report and official website, Company’s own publications- Different articles and various Business publications in the internet.
Company profile
ACI was established as the subsidiary of Imperial Chemical Industries (ICI) in the then East Pakistan in 1968. After independence the company has been incorporated in Bangladesh on the 24th of January 1973 as ICI Bangladesh Manufacturers Limited and also as Public Limited Company. This Company also obtained listing with Dhaka Stock Exchange on 28 December, 1976 and its first trading of shares took place on 9 March, 1994. Later on 5 May, 1992, ICI plc divested 70% of its shareholding to local management. Subsequently the company was registered in the name of Advanced Chemical Industries Limited. Listing with Chittagong Stock Exchange was made on 22 October 1995.
Advance Chemical Industries (ACI) Limited is one of the leading conglomerates in Bangladesh, with a multinational image. ACI is a Public Limited Company with a total number of 19,653 shareholders. Among these, there are three foreign and fifty local institutional shareholders. The company has diversified into three major businesses. Besides these, the company has a large list of international associates and partners with various trade and business agreements.
Strategic Business Units:
• Pharmaceuticals
• Consumer Brands & Commodity Products
• Agribusinesses
ACI has the following subsidiaries:
• ACI Formulations Limited
• Apex Leather crafts Limited
• ACI Salt Limited
• ACI Pure Flour Limited
• ACI Foods Limited
• Consolidated Chemicals Limited
• Premiaflex Plastics Limited Page 7
• Creative Communication Limited
• ACI Motors Limited
• ACI Logistics Limited
Joint Ventures:
• ACI Godrej Agro vet Limited
• Tetley ACI (Bangladesh) Limited
• Asian Consumer Care (Pvt.) Limited
• ACI Consumer Electronics
ACI MOTORS LIMITED
ACI Agribusinesses has launched a new subsidiary business, ACI Motors, from 6th November 2007 with an objective to market high quality farm machineries and light commercial vehicles. ACI Agribusinesses now ensures complete solution to the farmers with the introduction of the agro-machineries. ACI Motors are now marketing the various models of Sonalika tractor which is 3rd leading position in India as well as the fastest growing brand. It also has introduced high quality Bull Power brand power tiller and mini combine harvester, Hardy Sprayer from China. It has own sales and service center by which ensure highest quality after sales service, repairs and spare parts. It also provides flexible credit facilities for farmers for better customer satisfaction and service. ACI Motors are planning to introduce light commercial vehicles like pickups and mini trucks to support farmers to carrying agricultural goods. Also, high quality diesel engines and pumps for irrigation purpose will be offered in the near future. This business
shows considerable promise in contributing to the agricultural productivity of Bangladesh.
Product Profile
ACI Motors sell power tiller, pump, light pick-ups and mini trucks, tractors, diesel engine, harvester, rice transplanter, rice cutter, spray machine etc.

DISTRIBUTION NETWORK
The company maintains strategically located sales centers in nineteen different locations across the country. It has developed an advanced distribution system through its more than 300 skilled and trained manpower and a large fleet over eighty vehicles. The distribution system is capable of handling continuing volume of diverse range of products from the various businesses.
The company’s distribution centers are highly streamlined, computerized and automated. We are capable of maintaining a cold chain for some specialized range of products such as vaccines and insulin. The combination of this advanced function and multidimensional capabilities made it possible to handle hundreds of products efficiently.
COMPANY POLICY
ACI’s mission is to achieve business excellence through quality by understanding, accepting, and meeting exceeding customer expectations. ACI follows International Standards on Quality Management System to ensure consistent quality of products and services to achieve customer satisfaction. ACI also meets all national regulatory requirements relating to its current businesses and ensures that current Good Manufacturing Practices (CGMP) as recommended by World Health Organization is followed for its pharmaceutical operations.
The management of ACI commits itself to quality as the prime consideration in all its business decisions. All employees of ACI must follow documented procedures to ensure compliance with quality standards. The pool of human resources of the company will be developed to their full potential and harnessed through regular training and their participation in seeking continuous improvement of work methods.
Environment policy
ACI is committed to maintain the harmonious balance of our eco-system and therefore constantly seeks ways to manufacture and produce products in an eco-friendly manner so that the balance of nature remains undisturbed and the environment remains sustainable. In pursuit of this goal, ACI will:
• Comply fully with all local and national environmental regulations.
• Conserve natural resources like water and energy for sustainable development, and adopt environmentally safe processes.
• Ensure appropriate treatment of all effluents prior to discharge, to prevent pollution or
degradation of environment.
• Ensure appropriate communication and cooperate with internal and external interested parties on environmental issues.
• Create awareness on environmental issues among our employees and suppliers.
• Adopt modern waste management technology
BUSINESS ACTIVITIES
ACI Motors limited is a private Limited company incorporated in 2006 with the registrar of joint stock companies, Dhaka, Bangladesh under the company Act 1994 having 75% shares by Advanced Chemical Industries Limited ‘ACI Limited”. The principal activities of the company is buying, selling, importing and assembling of vehicles of both agriculture and other than agricultural use including supply spare parts and providing service facilities for vehicles.
TASK OF THE MARKETING DIVISION OF ACI MOTORS
Mechanized Cultivation is a basic requirement of Bangladesh. Farmers use tractors for land preparation and for transport of agriculture outputs to the Markets place. Farmers were not adequately supported to fulfill this need; their hardship was accentuated due to labor shortage. Furthermore mechanization would increase productivity, lead to uniform quality of land preparation, and reduce the time between crops. To fulfill this need ACI Motors started its operation on November 2007, with a wide product range of agriculture Machineries like tractors, power tillers and mini combine harvesters. We made a commitment to ensure supply of quality machineries and proper after sales service.
Educating the farmers, with a focus on Environment Friendly Practices, ACI has undertaken extensive programs to educate crop farmers all over rural Bangladesh in Good Agricultural practices. ACI has a team of agricultural experts working at the field all across the country, holding a range of technical training and field demonstrations. Their activities include:
CORPORATE SOCIAL RESPONSIBILITYP
• Field demonstrations on various methods of crop protection, that pose the least hazard for the environment
• Training on new technologies of cultivation ,for higher yield and new crops
• Training to channel partners (e.g. retailers and agricultural workers) and third parties (e.g. NGO workers)
ACI also has similar education programs for animal and poultry farmers. These include:
• Technical training on diverse aspects of farming, and on application of new technologies
• Farmers’ group meeting for sharing of learning and experience
• Free visits to farmers by veterinarians, to identify problems and give advices to individual farmers.
Outcomes:
• Raising the level of awareness among farmers on improving their agricultural output through application of new technology, encouraging them to share experiences with neighboring farmers and in the long run, developing educated farmers.
• Raising the education level and technical knowledge of channel partners and third parties who act as advisors to the farmers.
• Most importantly, making the farmers aware of ways to protect the environment from hazardous uses of chemicals on their farms, allowing them the opportunity for informed decision making
FINANCE AND PLANNING
• Corporate Finance
ACI Finance and Planning function is the nerve centre of the conglomerate. Being the nature of the structure, ACI Finance and Planning plays the centralized role in all kinds of financial and accounting services. Meaning it handles financial and accounting matters of not only ACI Limited but also of all of its subsidiaries supporting the mission and vision of the Group. The major areas of its activities include:
• Treasury
• Insurance and risk management
• Costing
• Credit Management
• Accounts payable management
• General accounting
• Taxation
• New business management
ACI finance is pioneering in introducing and implementing state of the art financial tools like electronic banking, integrated accounting systems, better foreign exchange management through hedging, derivatives etc. To allow us to excel in our performance ACI Finance has strong rapport with all the international and major local banks, non-financial institution including leasing companies.
Driving force of Finance is its motto which is “to become most value adding business partner”. To drive this vision, ACI Finance proactively helps business in providing right and timely information, analysis, budgetary management and participating in cross-functional team. The Planning function not only compiles and coordinate the company plan of the conglomerate but also instrumental in feeding the CEO and top team different macro and micro economic situation of the country as well as world in large. These in-depth analyses help the company to make correct and pragmatic decision as a part of strategic initiative.
The new business development area is one of the most exciting areas in ACI. Here we keep a track on potential areas of growth being envisaged in the country, these are followed by rigorous analysis and subsequently matching these with ACI’s competence. This allows ACI’s growth engine to get enough fuel to take its course forward.
Performance Measurement of ACI Motors
Agricultural Machineries business in Bangladesh
Agriculture Machineries Industry or business is not new in Bangladesh. This Business was started in 1962 with Deep tube well and Power Tiller by Pakistan Agriculture Development Corporation. After the independence of Bangladesh, This sector goes under the Ministry of Agriculture, Bangladesh and Bangladesh Agriculture Research Institute (BARI) and Department of Agriculture Extension (DAE) wings are the main supervisors or monitor of this sector. For the irrigation of the land water pump concept was introduced in 1974. Uses of power tiller diesel engine become popular during the beginning of 1982 with the investment of self interested people. The Chittagong Builders is one of them. After that by the withdrawal of import duty on agrimachineries in 1984, privatization of this sector gets more speed. Tractor was first introduced in Bangladesh in 1985 by The Metal Pvt Limited. But it started to get popularity from 1999.At present Total Tractor using population in our country is 20000. Agricultural Engineers of Bangladesh Agriculture Research Institution is working on the development of new technologies and its uses in Bangladesh for the betterment of our farmer and our agriculture sector. Up to now this institution successfully introduced many modern agrimachineries to the farmers like:– High Speed Rotary Tiller, Crop cutting Machine, Hand and Power operated corn Harvesting machine, Potato withdrawal Machine , Mango Picking and grading machine etc. This institution along with farmers also provides training to different companies on manufacturing, operating and
maintenance of these machines.
Current situation of ACI Motors:
ACI Motors started its operation with the product range of agriculture machineries like Tractor, Power tiller and Mini Combine Harvester and ensured supply of quality machineries and better after sales service.
ACI Motors are now marketing the various models of Sonalika Tractors of ITL which is 3rd leading position in India as well as the fastest growing brand. Sonalica tractor is especially designed which is suitable for Bangladesh small land size & roads. ACI has also introduced high quality ACI Power Tiller, ACI Diesel Engine from China, Daedong Combine Harvester & Rice Transplanter of Korea & ACI water pump from China considering Bangladesh perspective. All the brands introduce by ACI have received tremendous response from the farmers.
- In 2007 Introduced “Sonalika Tractors”
- In 2008 Introduced “Bull Power” Power Tiller
- In 2009 Introduced “Diesel Engine”
- In 2010 Introduced “Combine Harvester”
- In 2011 Introduced “Rice Transplanter”
- In 2011 Introduced “ACI Water Pump”
Competitors of ACI Motors:
In motors sectors Mahindra, TAFE for tractor, Chittagong builders and machinery for power tiller and Gazi, RFL, Partex for Pump.
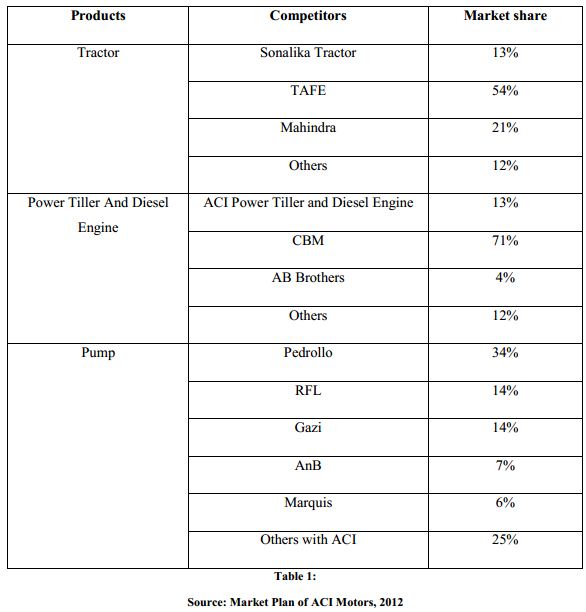
ACI Tractor:
The main competitors of ACI motors especially in the Tractor power tiller and Diesel engine sector are the Metal Private Limited (TAFEE tractor), Karnafuli Private Ltd, The Alim Industries Ltd. Metal Private Limited first introduced Tractor in our country. They are the sole distributor of Indian TAFE brand tractor. At present this company is the market leader in the tractor sector of Bangladesh. TAFE brand has a very good reputation in our country and this company has a very strong network all over Bangladesh. karnafuli Private Ltd distributor of Indian Mahindra tractors in Bangladesh. At present this Mahindra brand is holding number 2 position in the tractor industry of Bangladesh. ACI Motors Tractor “Sonalika” is number 3 position in Bangladesh and India.
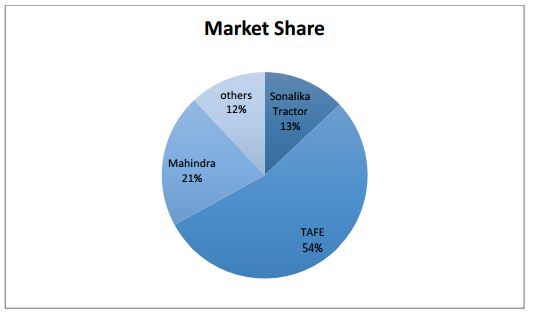
ACI Power Tiller and Diesel Engine:
In the early years only one company used to bring imported power tiller and diesel engine that is Chittagong Builders Ltd in Bangladesh. Chittagnong Builders and Machineries is the sole distributor of Chinese “Syfeng” brand power tiller and Diesel engine. Power tiller and Diesel engine of ‘Syfeng’ brand has a very good or in other words unbreakable reputation in the market.
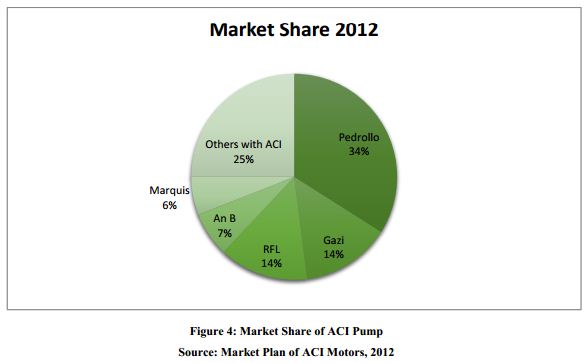
For this reason, the sales volume of chittagong builders is also very high comparing to others. Nowadays many companies are bringing power tiller and diesel engine from abroad. ACI Motors graps a good market share within short time because of their good quality products. The following figure shows the percentage of shares by different companies:
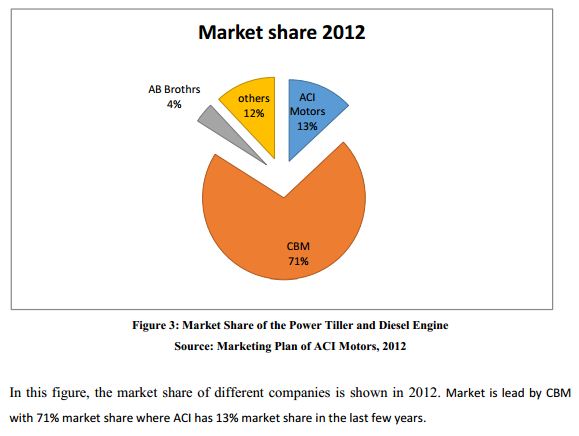
ACI Pump:
ACI Motors introduce pump in 2011, for this reason ACI has little market share in Pump Market. Pedrollo maintained their product quality as high from very beginning based on product life longevity with premium pricing. That’s why they are the market leader. Both Gazi & RFL compromised about product quality but insures the availability of after sales services with competitive pricing.
Customer of ACI Motors Products or Machineries:
An ACI motors has targeted different class or group of people for their different product or machineries. ACI Motors customers are dealers, rental service providers, user or farmer, mechanics, garden or farm owner and institutions. Science the price of tractor, power tiller combine harvester and Rice transplanter is quite and it is quite hard for an individual farmer to buy. For this reason ACI motors have targeted specific group of people. Like:
- Solvent farmers in a specific village who has quite a good amount land or under which lots of small farmers works.
- Businessman who want to invest money in new sector.
- People who return from different foreign country and want to do a profitable business.
- Different NGO’S who work with farmers like:Asha, Dipsikha, BRAC etc
- Delears of ACI Seed, Fertilizer (especially for Power tiller, Rice cutter, Diesel engine and sprayer)
However, price of Rice cutter, Diesel engine and sprayer is affordable to individual farmer. So, for selling these products individual farmers are also targeted by ACI Motors.
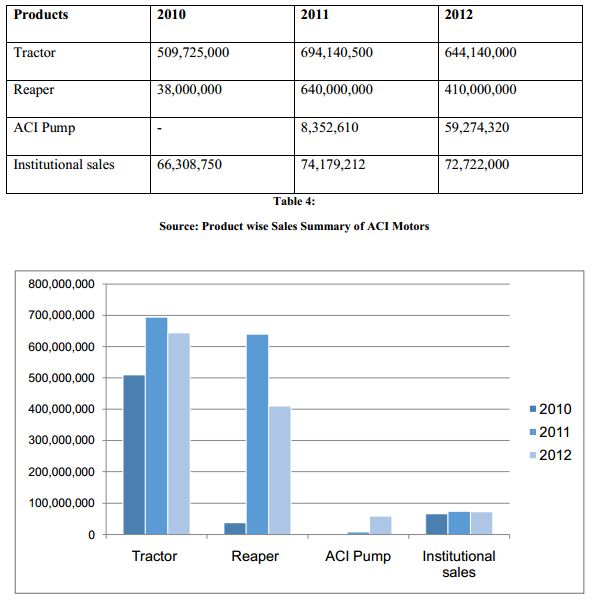
Sales value of product (BDT):
After Sell Service System of ACI Motors:
In this Agriculture Machineries sector after sale service plays a vital role for building a company’s reputation because in our country knowledge level of farmers or users about using agriculture machineries is very low. For this reason ACI motors has build up a strong after sales services and spare parts department headed with the service Manager, Service Engineer, Service Coordination Executive, Senior and junior Mechanics. The main objective of this department is to retain customer satisfaction. The total permanent manpower of ACI Motor after sales service and spare parts department is 45. Apart from these, ACI Motors also have some contractual mechanics. This department also gives their Service Engineers and mechanics to participate in different training program organized by Bangladesh Agriculture Research Institution where they learn how to operate and manufacture different types of new and light agricultural machineries.
Apart from these Service and spare parts department of ACI Motor organized training program for their service engineers and mechanics to increase their product knowledge and efficiency. Training is given by the expert Indian Service engineer of sonalika tractor. After selling of agrimachineries to customers Service engineer or mechanics of this department provide practical training to the customers about how to drive tractor, power tiller, how to maintain it properly, what should do and what should not to do etc. A written Bengali manual is also given at that time.
For Tractor Service department of ACI Motors provide 1 year free servicing or free servicing for using up to 1200 hours which one appears first.
Uniqueness of ACI Motors after Sales service department:
Provide maximum free service: Free servicing facilities of Sonalika Tractor start after 50 hours where other companies start this facility after 300 hour. Door to Door Service: It is a unique service providing system of ACI Motor after sell service department. In this system customers of ACI Motor give a call to the service engineer or
service Coordination Executive of his region and told his problem. After that, Mechanic of that Page 35 region will go to his house or mentioned place according to the promised schedule. Here, the customer does not have to take his machine or drive his machine to the showroom of his region.
WARRANTY POLICY FOR SONALIKA TRACTOR
• Warranty up to 12 months.
• Welding, machining, transportation, labor charges will not covered under warranty.
• Electrical items like bulb, Switches and glasses do not come under warranty.
• Filters, oil, gasket, hose pipe, Nut & bolts, Clutch Lining, Brake lining Plastic materials, Chain & Pins, front & rear wheel bearing are not included in the warranty.
Warranty is not applicable if tractor used in overload & poor maintenance.
Credit System through Tractor Business in ACI Motors
Hire purchase in ACI:
The target group of ACI motors is not that much although the user of ACI motors products is huge but big especially for Tractor, combine harvester and rice transplanted. So, 1 to 1 selling strategy is used by ACI motors. ACI motors have s 8 show room in Bangladesh for distributing and selling their machineries. ACI motor has showroom in: Comilla ,Dinajpur, Jessore, Bogra Rangpur, Sylhet, Barishal and Dhaka.
For identifying prospect, motivating them, projecting year to year sales ACI Motor has Territory Manger in each division, Marketing officer and more than 100 sales officers all over Bangladesh. Different models of Sonalika tractor is sold by 25%to 30% down payment of the total amount of the tractor. Rest of the amount is collected by 24 installments within 2 years with adding service charge from the customers. At the time of selling the tractor is registered on the name of ACI motors so that the company can take the tractor from customer if he failed to pay his installment. After completing the installment customers can register this tractor on his own name at his own
cost. ACI Motors has agreement with Krishi Bank and Markentile Bank and Agrani Bank from which customer can take loan for buying tractor.
Legal position:
Under company Act.1994 ACI Motors Limited is registered which facilitates formation of companies. ACI Motors Limited executes hire purchase agreement as per existing “Contract Law” 1972 and “Goods Sales Law” 1930 of Bangladesh.
Procedure of Hire purchase:
Customer selection:
The interested customer visits the nearby branch of ACI Motors and chooses suitable Tractor. They can buy the Tractor through the motor dealer or the company. The company provides application and asks them to fill it up. The company-investigating officers do enquiries, and customer credit worthiness is determined on the basis of the details given by the references. The customer needs to put Guarantor who provides security against loss, damages and any ensuing legal fees that can be incurred by customer. The customer has to give the photograph of himself and the guarantor, which would hold as a document to the agreement. After verifying all the necessary requirements of both the parties, ACI Motors allows the customer for buying the Tractor through hire purchase.
Following is a sample application form:

This application is verified through sales staff. Sales manager or monitoring officer, sales territory or territory manager is singed in the application form for verification. Credit limit amount and remarks will be recommended by the sales staff. He will also confirm whether the below documents are available or not.
Terms and condition of hire purchase
When ACI Motors enter into hire-purchase agreement, they give the following key information in writing to customer; otherwise the contract won’t be legally valid:
- The price of the goods in hire-purchase
- The amount of down payment that have to pay before delivery of Tractor.
- Information about the interest payable,
- The date each installment is to be paid. the annual interest rate and the method of charging it, the total interest to be paid, and the length of any interest-free term.
- The amount of each payment, the number of payments, when the first payment is due and how often the payments will be made after that Other fees and charges other than interest, such as registration fee, insurance fees, credit check fees, and security valuation fees, default fees that is, fees customer will have to pay if they don’t keep up their payments, fees may be charged if pay off the goods or loan early.
Basically there are two parties in the Hire purchase agreement, the intending seller (ACI Motors Limited) and the intending buyer or the hirer. Sometimes, it is involved three parties, the seller, the financier (The Bank) and the hirer. They finance the customers and get the interest. In this case ACI Motors Transfer the ownership to the name of bank, they deal the hire purchase agreement with the customer. The bank is authorized on behalf of the company. Bank collects the monthly collection and transfer the balance to the company. In return Bank gets commission from the company.
Parties are the Seller and the Buyer:
Owner: Seller is the person who sells the Goods to the Buyer. The Seller has entered into a factoring contract with the Factor and based on that the Seller has the right to assign the right of claim against the Buyer arising from the Contract to the Factor. ACI Motors Limited is the owner of Tractor.
Hirer: Buyer is the natural person who acquires the Tractor from the Seller under the terms and conditions of the Contract and is obliged to pay the Factor for it pursuant to the procedure.
Title and Ownership:
With regards to the ownership of the vehicle, the hirer holds the motor vehicle as a bailee of the owner and he shall not have any right, title or interest in the motor vehicle. There will a plate in the Tractor body written “ FINANCED By ACI MOTORS LTD.” It is used in the ordinary course of business as proof of ownership, possession or control of goods
Guarantee:
Guarantor is the very important and the third party to the agreement. He acts as a security to the hirer or the agreement. As per the agreement in case of the owner hiring out the vehicle to the hirer, guarantor agrees to fulfill all the obligations or responsibilities to be done by the hirer in case he fails to do so. The guarantor shall stand discharged of his obligations as the owner receives all amounts due owing and payable to the owner in pursuance of the agreement. He agrees that he shall be in full force and will be valid till the completed is charge of all liabilities of the hirer under this agreement.
Termination
When a customer fails to pay the minimum amount of due or installment on the payment due date, the account is considered in arrears or delinquent. When accounts are delinquent, collection of agreements:
At the natural end of a Hire Purchase contract, once all the contracted payments have been made, buyer can pay registration and purchase option fee take legal title to the car. Alternatively, they can choose not to pay this fee and register tractor by themselves. The branch manager approaches the divisional branch for termination of the agreement on satisfactory completion of the agreement. In case of foreclosure by the hirer, on his own volition the foreclosure amount as set by the divisional manager will be collected by the branch manager and paid to the zonal office. The branch manager after proper scrutiny hands over the termination papers to regional office. ACI Motors hands over the termination papers to the hirer effectively terminating the agreement
Collection Policy
Objective of Collection Unit is to build a cost effective Collection process which is risk aware, pro-active and information based. Its purpose is to assist business growth and maximize profitability by maintaining balance between risk and reward over the life-cycle of product. Customer has to pay installment every month to the account of ACI Motors.
Conclusion
To conclude I want to say that as a new company the performance of ACI Motors up to now is quite impressive. As, they have a very strong network which they build up with their working experience.
Hire purchase is one of the important types of financing a purchase of commercial vehicles. It is most preferred type of financing with its advantages over other types. Many companies are coming up with the hire purchase system to provide finance to the commercial vehicles and improving the economic standards by making the facility profitable and cost effective. ACI Motors Limited is one of the major players in Hire Purchase industry by providing truck finance to the small owners across the country.
ACI Motors is quite efficient in collecting their due debts and that they observe the collection periods given to each client although they rarely take their clients to court if default occurs, preferring to re-negotiate and assist in the client’s ability to pay.
Recommendation and Suggestion
- The hire purchase facility should be made easily available to the Farmer.
- The time allocation and installment size is not suitable for our Famer, they are not able to afford much money. So it will be very helpful for the farmer if ACI Motors increase the time for installment. It could be done extend their time for 5 years. By this farmer will get more time for return the debts and monthly installment size become small.
- The customer should not feel burden about the hire purchase installments, this should be realized by the company as the customer can provide with better provisions in payments.
- The company should help the customer in owning the advanced vehicles.
- The lending rates should be reasonable considering the economic condition of the society.
- ACI Motors is very efficient in keeping of the client’s records but are not quite willing in encouraging their clients to reconcile their statements. So it needs reconcile the customer about their terms and conditions.
- I think ACI should educate their clients about their hire purchase policies so that both the existing and potential clients wishing to apply for a hire purchase facility and buy the Tractor.
- It has threats a lot due to the high price of the ACI Motors Machineries and competitors are more comfortable because they are established. So, need to develop pricing strategy for increasing sells.
- Credit sale sometimes makes discrimination in the country business. So, it needs proper planning, strategy and full organizing capability.