Fundamental sciences is the study of material things was treated as a single aspect of human thought and called natural philosophy. But as knowledge increased it was found necessary to divide the study of nature into two main branches.
They are two main fundamental sciences are-
A. Physical sciences
B. Biological sciences
Physical science is the study of matter and energy. In physical science we study the properties of material i.e., metal, water, air etc. property is a feature of matter or the way it acts. Extreme hardness is the property of diamond. Black color is a property of coal and so on. Lemon juice taste sour. Perfumes evaporate easily. These are few examples of properties of different substances.
We also study force and motion; electricity, sound, thermal energy and light. We study energy transfer.
The two main physical sciences are
A. Physics
B. Chemistry
It is difficult to make a clear-cut distinction between the two, but, broadly speaking, chemistry deals with the action of one kind of substance on another while physics is connected mainly with matter in relation to energy
Biological sciences deal with living things, while the physical sciences are connected with the properties and behavior of non-living matter.
Physics
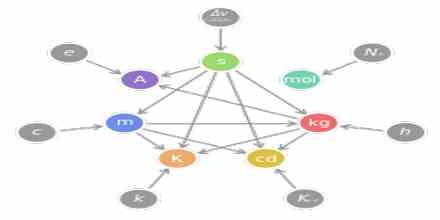
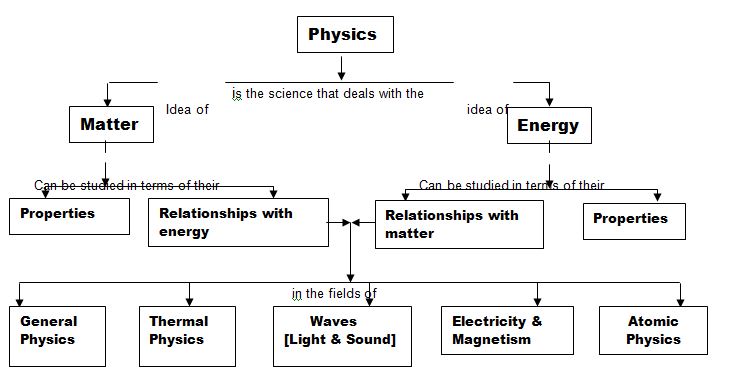
The study of physics looks into much of the natural world around us. It ranges from the astronomically large, such as solar system, to the microscopically small, such as the atom. Although the study of physics is commonly divided into major topics like General Physics, Thermal Physics, Waves, Electricity and Magnetism, and Atomic Physics all these topics are related to two main ideas: matter and Energy. Fig – 1 shows a simple concept map of physics.
MEASUREMENT OF PHYSICAL QUANTITY
Physical science is nothing but the basic knowledge of accurate measurement. Length, width, weight etc. are commonly measured quantities. These are all physical quantities. In physics physical quantity means a quantity that can be measured or the result of a measurement. Historically, people have always realized the need of standard weights and measures. From time to time these standards have been revised, improved and established by law.
Measurement
In general sense “To measure something using a standard unit and expressing it in terms of standard units is called measurement.” In physical science, by measurement we understand comparison of size, weight or other phenomenon of similar objects. For example, it we ask the salesman what is the size or length of a saree? Then the sales might measure the saree using his hands and say “the length of the saree is 11 cubit (hands)”. From this measurement, we understand that the length of the saree is 11 times the size of his forearm.
Units of Measurement
To measure any physical quantity a convenient fraction or standard of that quantity taken to which the quantity is compared with. This standard fraction is known as unit. In the preceding example, “hand” is used as a convenient fraction or standard in measuring the saree, which in physical science is called “unit”. In this example, the unit of length is “hand”. We shall learn details of the measurement units in the following topics Although in the previous example we have used “hand” as a unit of measurement for length, it cannot be accepted universally. Why? As the lengths of hands vary from person to person, the measurement would not be a standard one and would be faulty. We must adopt some quantity which is accepted unanimously all over the world.
Fundamental and Derived Quantities
Although there are many physical quantities in physics, only a few are required to express them. Generally, length, mass and time – these three quantities are called fundamental quantities. These quantities are not dependent on each other or any other quantities. For example, the distance from home to school is 1000 meters and it takes 180 seconds to get there. Now the average speed from home to school can be obtained by dividing the distance by the time.
Therefore, Speed = = = 5.55 meter/second.
We can see that using distance (length) and time we are able to calculate another quantity “speed”. In other words, the quantity ‘speed’ is dependent on two other quantities, length and time, but length and time are independent of each other. In fact, apart from length, mass and time the other quantities are made up of the combination of these three quantities. Since these quantities are derived from three fundamental quantities they are called “derived quantities”.
According to the dependence on measurements the physical quantities are divided into two types.
(a) Fundamental quantity and (b) Derived quantity
(a) Fundamental Quantity:
“Fundamental quantities are those which do not depend on other quantities, rather other quantities
depend on them”. For the purpose of measurements, scientists have identified four more
quantities other than mass, length and time as fundamental quantities. These are thermodynamic
temperature, luminous intensity, current and amount of matter.
(b)Derived Quantity:
“Derived quantities are those which depends on fundamental quantities and are derived from them.”
There are only seven fundamental quantities, but there can be numerous derived quantities; area,
volume, force, velocity, density are few of the derived quantities.
Base and Derived Units
We know that units are required to measure a quantity. Since quantities are divided into two group namely fundamental and derived quantities, units are also divided into two groups based on the same principle. They are (a) Base units and (b) Derived units.
Bellow are given two examples which explain and differentiate the two types of units. We know that, Area = length ´ Width.
According to the figure. Area of ABCD = AB ´ BC
Now, if AB = 3 meter and BC = 2 meter
Area of ABCD = 3 meter.2 meter = 6 square meter or m2.
Here, “Square meter” is the unit of area. If we know the unit of length, which is base unit (meter), we can find out the unit of area (square meter)
\Unit of Area = (unit of length) 2
Or, Square meter = (meter)2
\ Square meter or m2 is a derived unit.
To find the unit of speed we need to divide the unit of distance by the unit of time,
Hence, unit of speed =ms–1
So we can see that the units of distance and time, meter and second respectively are two fundamental units from which we can determine another quantity (speed), yet meter and second do not necessarily depend on units of other quantities.
In the light of above two examples we may define base unit and derived unit as follows.
Base Unit:
The units of fundamental quantities are termed as base units. In other words,
“The units of quantities which are not dependent on each other or on units of any other quantities, rather, can he used to make up units of other quantities, are called base units.”
Scientists have identified seven fundamental quantities. These are length, mass, time, thermodynamic temperature, current, luminous intensity and the amount of matter. So, these quantities also have seven different units and these are all base units. The units are meter, kilogram, second, Kelvin, ampere, candela and mole.
Derived Units:
The units of derived quantities are termed as derived units. In other words,
“The units which are based on the other base units are called derived units.’
There is no specific number of derived units since these can be made up of different combination of seven base units. For example, square meter, Newton, watt, etc.
Different Systems of Units
Different units are required to measure the quantities like length, mass and time. There are three different systems of units for measuring the fundamental quantities which are being used throughout the world. The systems are,
- C. G. S system : Under this system the unit of length is centimetre (cm), the unit of mass is gram(g) and unit of time is second(s). For this reason system is also called Centimetre-gram-Second system or in short C. G. S system.
- F .P. S system : Under this system the unit of length is foot(f), the unit of mass is pound(lb) and the unit of time is second(s). For this reason this system is also called Foot-Pound-Second system or in short F. P. S system.
- M. K. S system : Under this system unit of length is meter (m), unit of mass is kilogram (kg) and unit of time is second. For this reason this system is also called Meter-Kilogram-Second system.
The International System of Units
This system is abbreviated as S.I. from the French words ‘Le Systeme Internationale d’Unites’. The S.I. is maintained by the an agency called ‘The International Bureau of Weights and Measures’(BIPM) situated in Paris and it is updated every few years by an international conference, ‘General Conference on Weights and Measures’ (CGPM) attended by representatives of all the industrial countries and international scientific and engineering organizations. Under this system the selected seven fundamental quantities and their respective base units are given in the following table.
Table 1: Fundamental quantities and their S. I. units.
| Physical quantity | S. I. units | Symbol of unit |
| Length | Metre | m |
| Mass | Kilogram | kg |
| Time | Second | s |
| Temperature | Kelvin | K |
| Current | Ampere | A |
| Luminous Intensity | Candela | cd |
| Quantity of matters | mole | mole |
Scientific Notation: Use of Power of 10
Scientists often use such numerical values which can be very large or very small. For example, the speed of light is approximately 30,00,00,000 ms–1. The electrical charge in an electron is 0.00000000000000000016 coulomb.
Normally it is very difficult to count all the Zeroes in the previous two examples. These values are difficult to grasp, remember, read and write. We may conveniently use the power of 10 to eliminate this problem. For example, we may simply express the velocity of light as 3 ´ 108ms–1.
We know 100 = 1
101 = 10
102 = 100 (= 10 ´ 10)
103 = 1000 (=10 ´ 10 ´ 10) etc
The power is expressed as to how many zeroes are there after 1 and the raised power is termed as index. In the preceding example 0, 1, 2, 3 etc. are indices (plural of index). We may observe the similar procedure in case of numbers less than one.
10–1 = = 0.1
10–2 = = 0.01
10–3 = = 0.001
Here are some examples of converting some very big and very small numbers into scientific terms,
6733000000 = 6.733 ´ 109
0.00000846 = 8.46 ´ 10–6
The law of indices can be applied in expressing scientific notation. The laws are as follows:
10m ´ 10n = 10 m + n
here m, n can be either positive or negative e.g. e 106 ´ 107 = 106+7 = 101`3
107 ´ 10–20 = 107 + (–20) = 10 –13
For division, = 10n ´ 10–m = 10n–m
e.g. 106 ¸ 104 = 106–4 = 102
103 ¸ 10–7 = 103–(–7) = 1010 etc.
Table 2 : Multiples of Ten and their nomenclature in SI.
| Prefix | Multiple | Name | Symbol | Example |
| Peta | 1015 | Quadrillion | P | 1 petametre = 1 pm = 1015m |
| tera | 1012 | Trillion | T | 1 terahertz = 1 THz = 1012Hz |
| giga | 109 | Billion | G | 1 gigahertz = 1 GHz = 109 Hz |
| mega | 106 | Million | M | 1 megawatt = 1 MW = 106 W |
| kilo | 103 | Thousand | k | 1 Kilogram = 1 Kg = 103g |
| hecto | 102 | Hundred | h | 1 hectometre = 1 hm = 102m |
| deca | 10 | Ten | da | 1 decanewton = 1 da N= 10N |
| deci | 10–1 | Tenth | d | 1 decilitre = 1 dW = 10–1W |
| centi | 10–2 | Hundredth | c | 1 centimetre = 1 cm = 10–2m |
| milli | 10–3 | Thousandth | m | 1 milliampere = 1 mA = 10–3A |
| micro | 10–6 | Millionth | m | 1 microvolt = 1mV = 10–6V |
| nano | 10–9 | Billionth | n | 1 nanosecond = 1ns = 10–9s |
| pico | 10–12 | Trillionth | P | 1 Pico farad = 1 PF = 10–12F |
| femto | 10–15 | Quadrillionth | F | 1 femtometre = 1 fm = 10–15m |
Table 3: Symbols, units and dimensions of some important physical quantities.
Name of quantity | Symbol | Name of unit | Symbol of unit |
| Area | A | meter2 | m2 |
| Volume | V | meter3 | m3 |
| Velocity, speed | u | meter/second | ms–1 |
| Acceleration | a | meter/second2 | ms–2 |
| Momentum | P | Kilogram meter/second | kg ms–1 |
| Force | F | Newton | N |
| Work | W | Joule | J |
| Power | P | Watt | W |
| Energy | E | Joule | J |
| Density | r | kilogram/meter | kgm–3 |
| Pressure | P | Pascal | Pa |
| Wave length | l | Meter | m |
| Frequency | f | Hertz | Hz |
| Co-efficient of expansion | a,b,g | Per Kelvin | K–1 |
| Quantity of heat | Q | Joule | J |
| Heat capacity | C | Joule/Kelvin | J K–1 |
| Specific latent | l | Joule/kilogram- Kelvin | Jkg–1 K–1 |
| Heat Thermal conductivity | K | watt/ meter kelvin | Wm–1K–1 |
| Luminous intensity | l | Candela | cd |
| Luminous flux | j | Lumen | lm |
| Illumination | E | Lux | lx |
| Power of a lens | P | Dioptre | d |
Exercise
- Multiple Choice Questions :
Choose the correct answers from below :
1. Which one is not a fundamental quantity?
a. Time b. mass
c. Density d. length
2. Which one is not a derived quantity?
a. velocity b. force
c. temperature d. all
3. How many fundamental quantities are there?
a. 3 b. 7
c. 6 d. 8
4. The unit which can be found using fundamental units is called,
a. derived unit b. fundamental unit
c. C. G. S unit d. locally used units
5. Which unit system has resemblance with the international system unit?
a. C. G. S b. F. P. S
c. M. K. S d. All