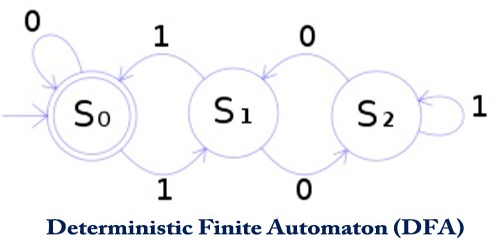
Deterministic Finite Automaton (DFA) also known as Deterministic Finite Acceptor (DFA), Deterministic Finite-State Machine (DFSM), or Deterministic Finite-State Automaton (DFSA) are finite state machines that accept or reject strings of characters by parsing them through a sequence that is uniquely determined by each string. It is a branch of theoretical computer science.
The term “deterministic” refers to the fact that each string, and thus each state sequence, is unique. In a DFA, a string of symbols is parsed through DFA automata, and each input symbol will move to the next state that can be determined.
A DFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where −
- Q is a finite set of states.
- ∑ is a finite set of symbols called the alphabet.
- δ is the transition function where δ: Q × ∑ → Q
- q0 is the initial state from where any input is processed (q0 ∈ Q).
- F is a set of final state/states of Q (F ⊆ Q).
A DFA is defined as an abstract mathematical concept but is usually implemented in hardware and software for solving various specific problems. As an example, a DFA can model software that decides whether or not online user input like email addresses are valid.
DFAs recognize precisely the set of standard languages, which are, among other things, useful for doing lexical analysis and pattern matching. DFAs will be built from nondeterministic finite automata (NFAs) using the facility set construction method.
- A DFA is represented by digraphs called state diagram.
- The vertices represent the states.
- The arcs labeled with an input alphabet show the transitions.
- The initial state is denoted by an empty single incoming arc.
- The final state is indicated by double circles.
DFAs today have become widespread in both computer and data science. Finite automata are used by most computer language compilers to assist in parsing and preparing code for actual use. Additionally, they are used extensively in language processing systems, including in natural language processing, to assist programs in understanding how to respond to unique and varied inputs.
DFAs are one of the most practical models of computation since there is a trivial linear time, constant-space, online algorithm to simulate a DFA on a stream of input. Also, there are efficient algorithms to find a DFA recognizing:
- the complement of the language recognized by a given DFA.
- the union/intersection of the languages recognized by two given DFAs.
DFAs, due to their inability to actively inhabit multiple states directly, also are essential in everything from password recognition algorithms (to determine whether a user’s input is correct or incorrect) to filtering algorithms and even in text processing applications. In data science, basic deterministic finite automata may be used as sorting tools when building data warehouses and other storage systems.
The first algorithm for minimal DFA identification has been proposed by Trakhtenbrot and Barzdin in and is called the TB-algorithm. However, the TB-algorithm assumes that all words from ∑ up to a given length are contained in either S+ U S–.
By parsing data as it arrives and determining its proper location, a DFA can automate an oversized portion of the sorting and do so significantly faster than manually performing the task. When combined with a Non-deterministic Finite Automaton (or NFA), data warehouses may ascertain whether data belongs in additional than one location. DFA and NFA are used separately to make a far broader and effective solution.
Information Sources: