About Boolean Algebra
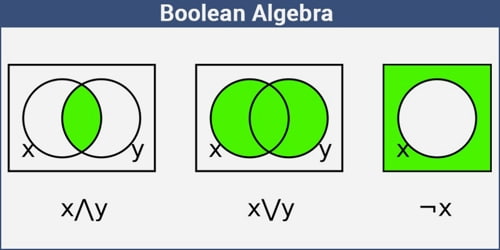
Boolean algebra is a type of mathematical operation that, unlike regular algebra, works with binary digits (bits): 0 and 1. While 1 represents true, 0 represents false. Instead of elementary algebra where the values of the variables are numbers, and the prime operations are addition and multiplication, the main operations of Boolean algebra are the conjunction and denoted as ∧, the disjunction or denoted as ∨, and the negation not denoted as ¬. It is thus formalism for describing logical relations in the same way that elementary algebra describes numeric relations.
It provides a set of rules (called Boolean logic) that are indispensable in digital computer-circuit and switching-circuit design. Boolean operation is carried out with algebraic operators (called Boolean operators), the most basic of which are NOT, AND, and OR. These three simple operations—NOT, AND, and OR—are actually all we need to know about Boolean algebra in order to understand how computers and calculators add numbers.
Boolean algebra is named for George Boole, a mathematician who first described it in 1847. According to Huntington, the term “Boolean algebra” was first suggested by Sheffer in 1913, although Charles Sanders Peirce in 1880 gave the title “A Boolian Algebra with One Constant” to the first chapter of his “The Simplest Mathematics”.
Following are the important rules used in Boolean algebra.
Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.
Complement of a variable is represented by an overbar (-). Thus, complement of variable B is represented as. Thus if B = 0 then = 1 and B = 1 then = 0.
ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.
Logical ANDing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometime the dot may be omitted like ABC.
A law of Boolean algebra is an identity such as x∨(y∨z) = (x∨y)∨z between two Boolean terms, where a Boolean term is defined as an expression built up from variables and the constants 0 and 1 using the operations ∧, ∨, and ¬. The concept can be extended to terms involving other Boolean operations such as ⊕, →, and ≡, but such extensions are unnecessary for the purposes to which the laws are put. Such purposes include the definition of a Boolean algebra as any model of the Boolean laws, and as a means for deriving new laws from old as in the derivation of x∨(y∧z) = x∨(z∧y) from y∧z = z∧y as treated in the section on axiomatization.
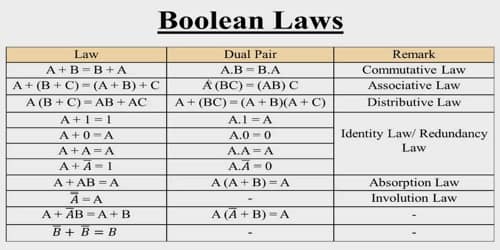
An identity is a statement true for all possible values of its variable. The first Boolean identity is that the sum of anything and zero is the same as the original. Below you can see some basic identities of the Boolean algebra for the variable A.
Additive Identity
A + 0 = A
A + 1 = 1
A + A = A
Multiplicative Identity
A * 0 = 0
A * 1 = A
A * A = A
Boolean algebra as the calculus of two values is fundamental to computer circuits, computer programming, and mathematical logic, and is also used in other areas of mathematics such as set theory and statistics.
In the early 20th century, several electrical engineers intuitively recognized that Boolean algebra was analogous to the behavior of certain types of electrical circuits. Claude Shannon formally proved such behavior was logically equivalent to Boolean algebra in his 1937 master’s thesis, A Symbolic Analysis of Relay and Switching Circuits.
Today, all modern general purpose computers perform their functions using two-value Boolean logic; that is, their electrical circuits are a physical manifestation of two-value Boolean logic. The most common computer architectures use ordered sequences of Boolean values, called bits, of 32 or 64 values, e.g. 01101000110101100101010101001011.
Information Source: