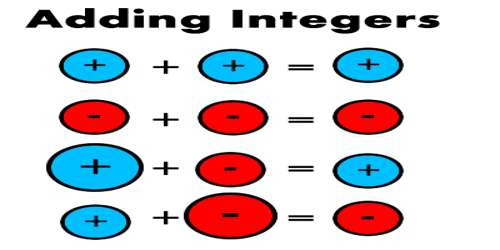
Adding Positive and Negative Integers
If one of the integers is negative, subtract the absolute value of it from the other number. Example: 14 + (-6) = 14 – 6 = 8
If both of the integers are negative, add their absolute values and prefix the number with a negative sign.
Rule 1: Adding positive numbers to positive numbers—it’s just normal addition.
For example: this is what you have learned all along. 3 + 2 are two positive numbers. You can calculate these problems the way you always have: 3 + 2 = 5.
Rule 2: Adding positive numbers to negative numbers—count forward the amount you’re adding.
This is where it gets a little harder. Pay close attention to where the negative signs are placed in the problem.
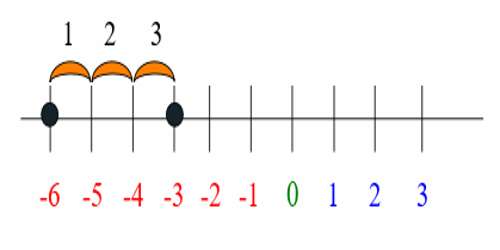
For example: -6 + 3. This would reading “negative six plus three”. The best way to think about this problem is to use a number line that extends to the negative numbers.
You’re starting with the negative number -6.
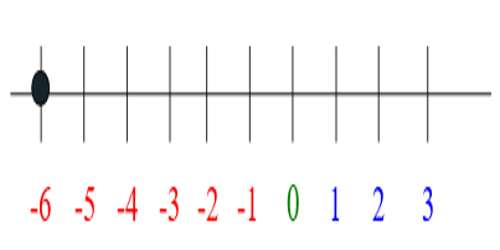
And you’re adding three to that number, which means you are moving three spots to the right.
The answer is -3. -6 + 3 = -3.
Rule 3: Adding negative numbers to positive numbers—count backwards, as if you were subtracting.
Now, let’s look at the reverse equation. When you are adding a negative number to a positive number you are effectively subtracting the second number from the first.
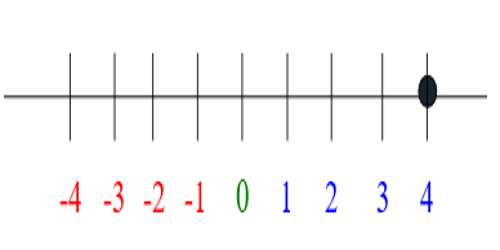
For example, take 4 + (-2). How does that look on the numbers line?
You start at 4.
And then you add the negative number, which means you are moving to the left – in the negative direction. Basically you are subtracting the 2.
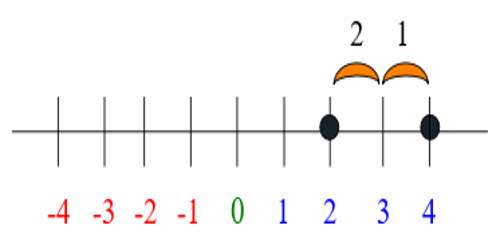
The answer is 2. 4 + (-2) = 2.
Rule 4: Adding negative numbers to negative numbers— treat the problem like subtraction (counting backwards).
When you are adding a negative number to a negative number, it becomes subtraction, where you start from a negative point on the numbers line and move left.
For example, -3 + (-2). This reads “negative three plus negative 2”. You need to ignore the plus sign and recognize that the second negative means you are subtracting that number.
We’re starting at -3.
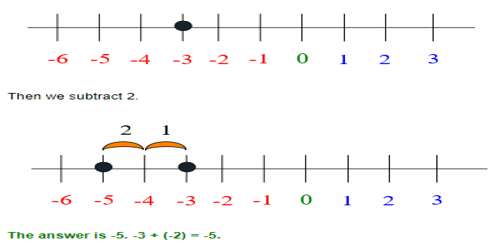
Information Source: