Additive inverse of a Number
The Additive Inverse Axiom states that every real number has a unique additive inverse. Zero is its own additive inverse. The sum of a number and the Additive Inverse of that number is zero.
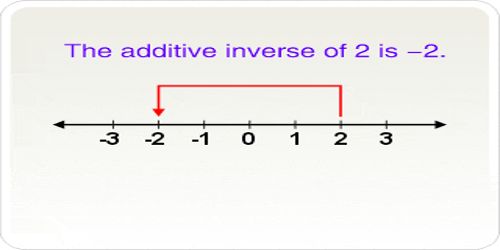
The additive inverse of a number ‘a’ is the number that, when added to a, yields zero. This number is also known as the opposite (number), sign change, and negation. For a real number, it reverses its sign: the opposite to a positive number is negative, and the opposite to a negative number is positive. Zero is the additive inverse of itself.
The additive inverse of ‘a’ is denoted by unary minus: −a. For example, the additive inverse of 7 is −7, because 7 + (−7) = 0, and the additive inverse of −0.3 is 0.3, because −0.3 + 0.3 = 0.
Example: The additive inverse of x is -x and when they are added together their sum is zero. x + (-x) = 0
Example: The additive inverse of -12 is 12 and when they are added together their sum is zero. (-12) + 12 = 0

Explanation:
The additive inverse of a number is what you add to a number to create the sum of zero. So in other words, the additive inverse of x is another number, y, as long as the sum of x + y equals zero. The additive inverse of x is equal and opposite in sign to it (so, y = -x or vice versa). For example, the additive inverse of the positive number 5 is -5. That’s because their sum, or 5 + (-5) = 0.
What about the additive inverse of a negative number? Using the same approach, if x is a negative number, then its additive inverse is equal and opposite in sign to it. This means that the additive inverse of a negative number is positive. For instance, if x equals -12, then its additive inverse is y = 12. We can verify that the sum of x + y equals zero, since when x = -12 and y = 12, we have -12 + 12 = 0.
It should be noted that the additive inverse of 0 is 0. Zero is the only real number, which is equal to its own additive inverse. It is also the only number for which the equation x = -x is true.
Information Source: