Angle between Two Skew Lines
Skew Lines mean two or more lines which have no intersections but are not parallel, also called agonic lines. Since two lines in the plane must intersect or be parallel, skew lines can exist only in three or more dimensions.
A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron. Two lines that both lie in the same plane must either cross each other or be parallel, so skew lines can exist only in three or more dimensions. Two lines are skew if and only if they are not coplanar.
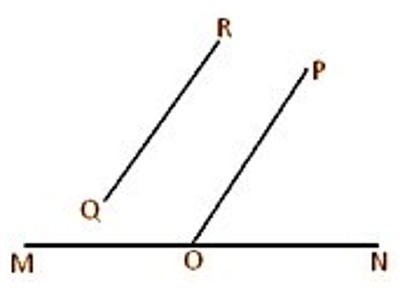
In geometry, Skew Lines are two or more non-parallel lines or curves that do not intersect. In 2-dimensional Euclidean geometry, there are no skew lines. In 3 or higher dimensions, there is an infinite number of skew lines. The angle between two skew lines (i.e., two non-co-planar straight lines) is measured by the angle between one of them and a straight line drawn parallel to the other through a point on the first line. In the given figure, let MN and QR be two skew straight lines. Take any point O on the line MN and draw the straight line OP parallel to QR through O. Then ∠NOP gives the measure of the angle between the skew straight lines MN and QR.
A triangle is a plane figure since all its three sides lie in one plane. Similarly, a parallelogram is also a plane figure. But a quadrilateral may or may not be plane figures since all its four sides always do not lie in one plane. A quadrilateral whose two adjacent sides lie in one plane and other two adjacent sides lie in a different plane is called a skew quadrilateral.
Information Source: