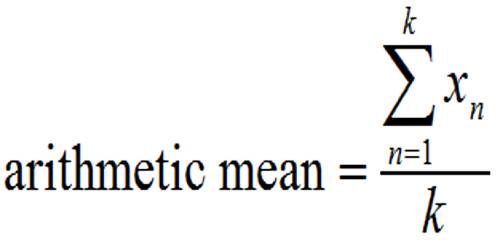The arithmetic mean, also called the average or average value, is the quantity obtained by summing two or more numbers or variables and then dividing by the number of numbers or variables. The arithmetic mean is important in statistics.
The arithmetic mean of a continuous function over a defined interval is determined by first calculating the definite integral over the interval, and then dividing this quantity by the width of the interval.
Sample problem: Find the arithmetic mean for average driving speed for one car over a 6 hour journey: 54 mph, 57 mph, 58 mph, 66 mph, 69 mph, 71 mph
- Step 1: Add all the numbers up: 54 + 57 + 58 + 66 + 69 + 71 = 375.
- Step 2: Divide by the number of items in the set. For this set there are 6 numbers, so: 375 / 6 = 62.5.
- Answer: The average driving speed is 62.5 mph.
When given three quantities are in Arithmetic Progression, the middle one is known as the arithmetic means of the other two.
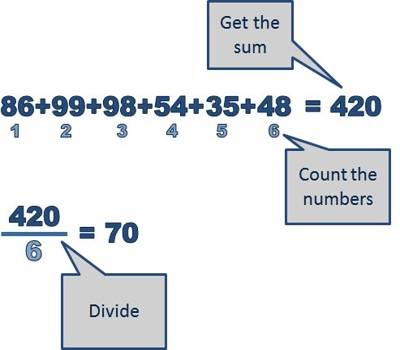
Examples of Arithmetic Mean:
(i) In the Arithmetic Progression {12, 22, 32}, 22 is the arithmetic mean between 12 and 32.
(ii) In the Arithmetic Progression {7, 9, 11}, 9 is the arithmetic mean between 7 and 11.
(iii) In the Arithmetic Progression {-5, 6, 17}, 6 is the arithmetic mean between -5 and 17.
(iv) In the Arithmetic Progression {-8, -12, -16}, -12 is the arithmetic mean between -8 and -16.
Let m be the arithmetic mean of two given quantities x and y. Then, x, m, y are in Arithmetic Progression.
Now, m – x = y – m = common difference
⇒ 2m = x + y
⇒ m = (x+y)/2
Therefore, the arithmetic mean between any two given quantities is half their sum.
If more than three terms are in Arithmetic Progress, then the terms between the two extremes are called the arithmetic means between the extreme terms.
Examples on arithmetic means between the extreme terms:
(i) In the Arithmetic Progression {3, 7, 11, 15, 19, 23, 27, 31, 35} the terms 7, 11, 15, 19, 23, 27 and 31 are the arithmetic means between the two extreme terms 3 and 35.
(ii) In the Arithmetic Progression {-5, -2, 1, 4, 7, 10, 13, 16, 19} the terms -2, 1, 4, 7, 10, 13 and 16 are the arithmetic means between the two extreme terms -5 and 19.
(iii) In the Arithmetic Progression {85, 80, 75, 70, 65, 60, 55, 50, 45} the terms 80, 75, 70, 65, 60, 55, and 50 are the arithmetic means between the two extreme terms 85 and 45.
Information Source: