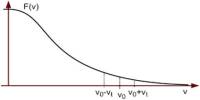
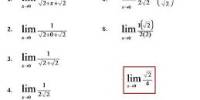A sequence of numbers is known as an arithmetic progression (A.P.) if the difference between the term and the preceding term is always same or constant. An arithmetic progression is a sequence of numbers such that the difference between any two successive members is constant.
For example,
- the sequence 1, 2, 3, 4, … is an arithmetic progression with common difference 1.
- Second example: the sequence 3, 5, 7, 9, 11,… is an arithmetic progression with common difference 2.
- the sequence 20, 10, 0, -10, -20, -30, … is an arithmetic progression with common difference -10.

Arithmetic Progression Formula
- Let ‘a’ be the first term and ‘d’ the common difference of an Arithmetic Progression. Then its
(i) General term (nth term) = tn = a + (n – 1)d
(ii) The sum of the first n terms = Sn = n/2(a + l) = [Number of terms / 2] (First term + Last term)
or, Sn = n/2 [2a + (n – 1)d] where l = last term = nth term = a + (n – 1)d.
- (i) The sum of first n natural numbers (S2)= n/2(n + 1)
i.e., 1 + 2 + 3 + 4 + 5 + ……………….. + n = n/2 (n + 1)
(ii) The sum of the squares of first n natural numbers (Sn)= 1/6 n (n + 1)(2n + 1)
i.e., 12 + 22 + 32 + 42 + 52 + ………………. + n2 = 1/6 n (n + 1)(2n + 1)
(iii) The sum of the cubes of first n natural numbers (S2) = {1/2 n (n +1)}2
i.e., 13 + 23 + 33 + 43 + 53 + ……….. + n3 = {1/2 n (n +1)}2
- The arithmetic mean between two given quantities ‘a’ and ‘b’ = ½ × (Sum of the given quantities) = a+b2a+b2.
- (i) If the sum of three terms in Arithmetic Progression be given, assume the numbers as a – d, a and a + d. Here common difference is d.
(ii) If the sum of four terms in Arithmetic Progression be given, assume the numbers as a – 3d, a – d, a + d and a + 3d.
(iii) If the sum of five terms in Arithmetic Progression be given, assume the numbers as a – 2d, a – d, a, a + d and a + 2d. Here common difference is 2d.
(iv) If the sum of six terms in Arithmetic Progression be given, assume the numbers as a – 5d, a – 3d, a – d, a + d, a + 3d and a + 5d. Here common difference is 2d.
Information Source